Death by Falling

 [Edit: If you're looking for real information on deaths by falls, see my next two posts here and here.]

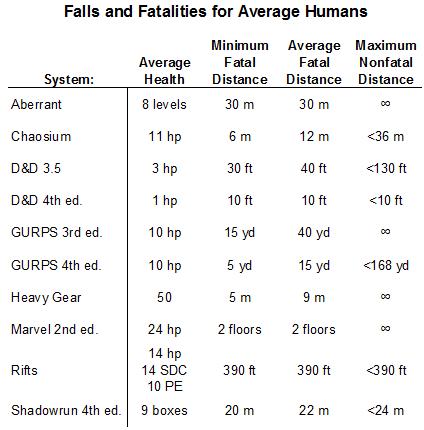
This is the first of several posts I have planned about simulating the results of falls from elevations.  Here I simply determined the minimum distance necessary to fall for an average human to die, the distance at which an average person would die on average, and the maximum distance that an average person could fall without dying for ten different systems.

As you can see, there are wide differences among systems.  The grades I give are subjectively based on how each mechanic models reality and contributes to game balance.

• Aberrant: For any fall under 30 meters, even the most feeble person has a 99.6% chance of only sustaining minor injuries that will heal in a day (bashing damage).  At 30 meters, damage becomes lethal and maxes out at 10 dice (an average of 4 levels of damage), with only a 1.3% chance of dying even when falling miles.  F
• Chaosium: Average health is actually 12hp, not 11, but the distances are correct.  1d6 damage for each 3 meters gives us a nice distribution of injuries and chances of death up to the assured death point at 36 meters. B
• D&D 3.5 (OGL): The average human in this system has 1d4 hp, which I round up to 3, but does not die until reaching -10 hp.  Most falls that are not immediately fatal will still result in wounds that may result in a person's eventual death if not stabilized, but I did not calculate that.  B
• D&D 4th ed.: The most appropriate stats I found for a non-heroic person in this game were for "Human Rabble", who have 1 hp.  At 1d10 damage for each 10' fallen, everybody dies from any fall of at least 10'. D
• GURPS 3rd ed.: Damage involves rolling 1d6 and subtracting a constant for each yard fallen.  Since it is possible to roll the constant or less on each 1d6, it is possible to take no damage at all when falling from any height.  Instant death requires 6xHealth damage in the GURPS systems. D
• GURPS 4th ed.: Now there is an equation for determining how many d6 to roll based on velocity.  GURPS in one of the few systems that takes acceleration into account instead of just distance.  A-
• Heavy Gear: Roll 1d6 for each meter up to 10 meters, and multiply the result by meters fallen up to 30.  Remember that the Silhouette system is funky, so "result" means the highest number rolled among the dice, and additional 6s each add 1 to the first 6.  It is possible (ridiculously unlikely) to roll all 1s and survive any fall.  It is also possible (ridiculously unlikely) to roll all 6s and die falling 5 meters.  An average person has a 40% chance of death falling 8 meters, and an 81% chance of death falling 9 meters. B-
• Marvel Super Heroes 2nd ed.: The rules as written were clearly not proofread or edited.  They make absolutely no sense in the English language.  On page 21 the rules say to take 1 point of damage for each floor fallen (a person would have to fall 24 floors), but also say to treat falling as a charge attack.  Charge attack rules on page 27 gave me the numbers I use for this post.  Using the Empire State Building for reference, I decided that a "floor" is 12 feet. F
• Rifts: People take 1 point of damage for each 10' fallen.  Instant death is at -(PE+1) hp.  A healthy average person will survive any fall under 390'.  F
• Shadowrun 4th ed.: I did not find stats for an average human.  Humans have 1-6 body points, bought up from 1 at character creation.  Looking at sample characters, I figured that an average human has a body of 2. Damage from falls over 6m is about (distance+4)/2, and characters roll (Body)d6 to resist some damage.  For someone with a Body of 3, the distances are 22m, 24m, 28m.  C
• 7th Sea: This is a game focused on dramatic swashbuckling stories, and seems to not have rules for falls.  

And here is a graph:

What Systems Do I Like?

People often ask me, "Why aren't you wearing any pants?"  Less often, they ask, "What is your favorite role-playing game?"  That is a slightly complicated question.  By which criteria do I judge RPGs?  The focus of this blog is their game mechanics, but a game may be a favorite based on the quality of the setting or how much fun with friends the game creates independently of mechanics and setting.  Here are the RPGs I am familiar with, and how I feel about them:

• Mutants and Masterminds:  This is my favorite right now. I have been very impressed with M&M's game mechanics.  It fixes nearly all of the problems I have with the d20 system (OGL 3.5).  There are some opportunities to min-max and create incredible powers, but an attentive GM can easily prevent it.  I love the superpower setting, but the mechanics can actually be applied to recreate most other settings.  I was impressed by Green Ronin for this game, and was looking for information on the 3rd ed. at their website when I found this article by their designer of the Dragon Age TTRPG in which he agrees with my own conclusion about die rolls.
• Action!: This free system by Gold Rush Games comes with instructions on customizing it!  I just stumbled upon this recently and have not played it, but it incorporates mechanics that I would use if I were creating a system.  It is worth checking out.
• Aberrant: This game has some of the most broken mechanics, and the canon storyline railroads campaign plots, but I have had tons of fun playing supers in this setting with friends and watching moral and ethical dilemmas unfold.
• Vampire: the Masquerade: I LARPed (live-action role-played) this for many years with the last version of the rules and setting.  I have not seen the current edition.  I met a lot of people this way, though not all of them were good to meet.  LARPing is a great role-playing experience, and V:tM is the easiest way to experience this because it is so widespread.  It's the Dungeons & Dragons of LARP.  Role-playing with 50+ people at a time is a blast, and this game fosters social and political maneuvers, shifting alliances, and secrets for a fun game.  Many of the other White-Wolf LARPs (Changeling, Werewolf, Mage, Oblivion) were not as conducive.  A bad storyteller will rely on sending monsters in for the player characters to fight, but good storytellers have long-term NPCs infiltrate player factions and subtly construct mysteries to be solved, complete with red-herrings and ambiguous clues that lead to both conflict and collaboration.  The mechanics are not great.
• Dungeons and Dragons: This is the Microsoft of the RPG world.  New gamers tend to come in with D&D because it has such a broad and deep foundation.  So many people play because so many other people play, and if you want to get in on a game, it is easier to find players familiar with and owning materials for D&D.  I don't like classes in games because they are too constricting, and lead to conformity instead of creativity.  I don't like levels in games because they also prevent customization and realistic development.  I don't like hit points in games because they are wholly unrealistic, and seem to solely exist to support the level system.  D&D has classes, feats, and powers set in stone in their system so they can sell lots of books with more.  What I like is the mechanics to create whatever powers are desired so that players can create whatever they want from a core book.  The d20 provides a linear progression of probabilities of success.  I have played each edition of D&D since the late '80s because those were the games my friends were running (and once I had the materials to play with them, I also ran a campaign), but I have not been satisfied. 
• Heavy Gear: I played in one campaign about 13 years ago, and I remember it being fun, largely because of the group.  The mechanics are a little weird, and encourage some min-maxing, but are relatively simple and straightforward.  The setting is not totally sensible, but provides opportunities for some different styles of campaigns.  You can also play a flat-out tactical mech game.
• GURPS: I only got to play GURPS once, but I've made characters in anticipation of other games I was told would happen.  I like that it is generic and uses point-buys.  The skill system tries well to be a good simulation, which I like, but is not great for game balance.  I do not like that powers and equipment are individually determined by Steve Jackson Games instead of them also giving us a point system for creating them.
• Chaosium: I'm getting around to it.
• Shadowrun: Also, just sitting on my shelf.
• Rifts: Totally silly.  Thanks, Palladium. 

I've played a couple others over the years, but they did not leave impressions.  I know there are more that I would like to play, such as Big Eyes Small Mouth, Hero, Paranoia, and Amber.  I will keep picking at the books I've got, then get a hold of more mechanics to evaluate.

Lucky Dice

Do you have lucky dice?  This is a slightly modified version of something I wrote a couple years ago that I think has a place here.

I have encountered more than one gamer over the years who believes that he has lucky dice. These dice are reported to roll the highest damage, the most critical hits, and generally turn the player's characters into unstoppable juggernauts. Of course, I did not notice any disproportionate numbers of good or bad rolls. I argued with these players that their perceptions were tainted by the availability heuristic and confirmation bias. When they can more easily recall rolling good numbers with certain dice, they label the dice "lucky". Then, whenever those dice roll well, they say, "See? This proves the dice are lucky!" Whenever the dice roll poorly, they say, "That was a fluke! These lucky dice usually roll well.", and fail to store the failures for future recall, feeding back into the availability heuristic. Well, there is a relatively easy way to determine if a die is lucky.

If you think you have a lucky die, record what it rolls EVERY TIME. If you believe it is lucky only in a certain situation (e.g.: "This is my saving-throw die!"), then record what it rolls every time you roll it in that situation. Do not leave out any rolls. There are no Mulligans. When you have a good amount of rolls (at least 30, but more is better), you can calculate the z-score for them, then compare that z-score to a threshold. This comparison is called a one-tailed test of proportion, and we use this specific type of comparison to test the hypothesis that your die rolls a higher (not just different) proportion of good rolls than a fair die. Though there are different ways to calculate the z-score based on how sure you want to be of the results, the following simple examples should be good enough for most of you.

The equation for z is:
z = (p - Po) / (sqrt((Po(1 - Po))/n))

The variables are:
p: the proportion of the rolls you recorded that were good (natural 20, 11 or higher, 8-10 on 1d10, etc...). p = ((# of good rolls) / (total # of rolls)).
Po: the proportion expected of fair dice (0.05 for a natural 20, 0.5 for 11 or higher on d20, 0.3 for 8-10 on d10). This should technically be written as pi subscript 0.
n: the total number of rolls you recorded

To make things easy, we will use an alpha of .05 in the examples (I explain further down). This gives us a threshold of 1.645. So, all you have to do is figure out z using the equation above (or one of the examples below), and if z > 1.645 you can claim that you may have a lucky die.

Example 1:
"My die rolls high."
Po = 0.5 (half of a fair die's rolls will be above the mean, and half below)
z = (p - 0.5) / (sqrt(0.25 / n))

Example 2:
"I roll 20s."
Po = 0.05
z = (p - 0.05) / (sqrt(0.0475 / n))

To elaborate on Example 1, let's say that I claim I have a d20 that usually rolls at least an 11, and I have countless stories of how it let my characters defeat monsters and overcome challenges. I want to prove to my naysayer friends that it really is lucky, so I write down every roll for a month. I rolled the die 100 times. 58 of the rolls were at least 11, and 42 were 10 or less. I get really excited about rubbing it in everyone's faces, but remember that there's more to do. After all, I only rolled the die 100 times, and even a fair die is likely to roll 58/100 good rolls eventually. Fair dice are only expected to roll exactly 50/50 as the number of rolls approaches infinity. So, I plug in the variables:
p = 0.58
n = 100
Po = 0.5
z = (0.58 - 0.5) / (sqrt(0.25 / 100)) = 1.600
1.600 < 1.645 (our threshold)
We should probably not be impressed that 58 of the rolls were above average. If the die had rolled 59 good rolls out of 100, z would have been 1.800.  What would that mean?

This is where I need to explain about alpha. In this case, alpha is the probability that you have a fair die even if z is greater than the threshold. Usually, an alpha of 0.05 lets us feel confident enough that the effect we have observed is based on the properties of what we are observing instead of a statistical fluke of the sample of observations.  It is easy to increase our confidence by using a smaller alpha, such as 0.01 (which would increase the z threshold), but using a smaller alpha increases the probability that we falsely think a lucky die is fair. There is a trade-off between the risks. Personally, I would demand a high degree of confidence, and would insist on an alpha of at most 0.01.  The best way to manage both risks of false results is to get a bigger sample of rolls. So, if you want to be more sure of whether your die is lucky or not, record 200 rolls, or 500. The bigger n gets, the better.


When alpha is 0.01, the z threshold is 2.328, so even 59% good rolls does not make me confident that the die is lucky.  For an alpha of 0.01, 62 out of 100 rolls would have to be above average.
To elaborate on Example 2, let's find out how many natural 20s have to be rolled with an alpha of 0.01 for someone to tell me that he rolls 20s.  
(p-0.05)/(sqrt(0.0475 / 100)) > 2.328
(p-0.05)/0.0218 > 2.328
p-0.05 > .0507
p > .1007
You would have to roll 11 20s out of 100 rolls.


Good luck.

Graphs of Success Probability by Skill Total and Difficulty

I've given you tables of success probabilities by skill total and difficulty for two systems (World of Darkness, Shadowrun 4th ed.), plus a graph for Heavy Gear.  Here I present that information again in graphs, plus two more systems, to show some of the different patterns that exist for success probabilities with increases in skill among different systems.

Linear

Here is your standard d20 system, most popular in Dungeons and Dragons.  Each character has a skill modified by an attribute and various other junk, added to a d20 result and compared to a difficulty level.  Each increase in the skill total raises the probability of success by 5% linearly.  There is always at least a 5% chance of failure (rolling a 1).  In the D&D games, skills are not bought with general character development points, but characters are alloted a few points each level to be used only for skills.  Difficulty levels typically scale with character levels, so it behooves players to specialize in a few skills that are always increased with the character level in order to maintain good probabilities of success as characters level up.  I am not getting in to "taking 10" or "taking 20".

Inconsistent

Here is the graph for Dream Pod 9's Silhouette system, used in their Heavy Gear game.  We can see that the progression is not consistent.  The lowest skill is concave, rapidly dropping the probability of success at low difficulties relative to the drop at higher difficulties where the probability of success is already very low.  A skill of 1 has a linear descent.  Higher skills progressively maintain high success rates among lower difficulties before rapidly plunging at higher difficulties, and then there is the bent tail as it becomes more possible to roll multiple 6s.  Attribute bonuses are added to skill roll results, shifting the graph to the right without changing its shape.

Normal

Isn't that pretty?  I am not sure if I am completely representing the GURPS system accurately here, but I think players just have to roll lower than the characters' skills on 3d6 to succeed at tasks (17s and 18s fail).  So, there is no real "difficulty level" for tasks other than what is forced by skill levels.  There may be modifiers that increase or decrease a skill for the purpose of a challenge, shifting the whole curve to the left or right.  If we graphed the probabilities of each individual outcome for 3d6, the line would be shaped like a bell.  I call this "normal" because as a "normal distribution" it has higher probabilities of outcomes in the middle, progressively less likely outcomes away from the middle, and is relatively symmetrical.

Inconsistent Normal

We can see here that both Shadowrun by Catalyst Game Labs and World of Darkness by White Wolf approach the normal curve as their dice pools (skill total, or skill + attribute) increase.  With few dice in these systems, it is impossible to approximate the distribution of the normal pattern, and the results more follow the Inconsistent pattern.  These systems both involve rolling multiple dice (d6 and d10, respectively), and counting die results over a threshold as "successes".  Players need a number of successes equal to a task's difficult in order to succeed.  So, the terminology can get annoying as people get a bunch of successes but still fail at a task.

I really like how the Normal distribution of probabilities of success works in simulations, but not necessarily the way that GURPS implements it in the absence of difficulty levels.  In real life, when we encounter tasks far below our skill level, we are quite likely to succeed at them and have a low variance with our high success rate.  When we encounter tasks far above our skill level, we are quite likely to fail at them and have a low variance with our high failure rate.  Tasks closer to our skill level have increasingly variant success rates.  Because of this, I am in favor of the use of normal distributions of probability of success in simulation systems.  This typically requires rolling more than one die and summing the results.