I've done a bit on the probability of death from falls from heights in the real world, and the average height a character would have to fall in order to die in various simulation systems. Here is a closer look at how the Aberrant system specifically compares to real life.
If you can even see the short blip at 30+ meters, you can understand how spectacularly Aberrant fails to simulate death by falling. The average person has 8 health levels, but there are two types of damage. Bashing damage hurts, lethal damage kills, and additional bashing damage becomes lethal damage after all 8 health levels have been damaged. Damage from falls under 30 meters is bashing. 1 die is rolled for each 3 meters fallen, and there is a 40% chance of each die resulting in damage. So, a 3 meter fall results in rolling 1 die with a 40% chance of suffering 1 level of bashing damage. A 29 meter fall results in rolling 9 dice with a very tiny chance of taking 9 levels of bashing, which converts to 7 bashing and 1 level of lethal damage, but a still-alive character. At the 30 meter level and above, however, 10 dice are rolled and all damage is lethal. This gives us a whopping 1.4% chance of death for everyone for all heights over 30 meters. This game is notorious for needing house rules, and I encourage game masters to crank up the falling damage in their campaigns.
I analyze, evaluate, and comment on tabletop role-playing game (RPG) mechanics. I address issues of game balance, simulation accuracy, min-maxing, and optimization.
Dec 14, 2011
Oct 7, 2011
Marvel Super Heroes - Strength and Lifting
It is time to see how Marvel Super Heroes weighs in as a simulator of human lifting abilities. Marvel includes the character creation mechanic of randomly generating the strength attribute such that half of characters are Typical, 20% are each of Poor and Good, and 5% are each of Feeble and Excellent.
Marvel is another system, like Shadowrun, that requires a roll to determine how much a character can lift in a particular moment, and there is wide variance. On average, a character of feeble or poor strength in Marvel can not lift anything, which is quite unrealistic. On average rolls, characters of typical and higher strength can lift about as much as real people can.
The above graph shows the maximum amount that Marvel characters can lift given really good rolls on d100. The maximum lift is a rare event in the game. In the game, 5% of people have a 6% chance in any given moment to lift 2000 lbs, which is double the most that any real person has ever lifted. The top quarter of Marvel characters is able to lift 800 lbs sometimes, which only a bare handful of men in the real world can accomplish. It is also easily possible (45%) for a stronger than average character to fail to pick up a measly 50 lbs, which is ridiculous.
Again, I am opposed to such wide variance within a character's moment-to-moment lifting ability. Marvel may even be a worse simulation than Shadowrun.
Marvel is another system, like Shadowrun, that requires a roll to determine how much a character can lift in a particular moment, and there is wide variance. On average, a character of feeble or poor strength in Marvel can not lift anything, which is quite unrealistic. On average rolls, characters of typical and higher strength can lift about as much as real people can.
The above graph shows the maximum amount that Marvel characters can lift given really good rolls on d100. The maximum lift is a rare event in the game. In the game, 5% of people have a 6% chance in any given moment to lift 2000 lbs, which is double the most that any real person has ever lifted. The top quarter of Marvel characters is able to lift 800 lbs sometimes, which only a bare handful of men in the real world can accomplish. It is also easily possible (45%) for a stronger than average character to fail to pick up a measly 50 lbs, which is ridiculous.
Again, I am opposed to such wide variance within a character's moment-to-moment lifting ability. Marvel may even be a worse simulation than Shadowrun.
Sep 26, 2011
Shadowrun 4th Ed. - Strength and Lifting
In Shadowrun 4th Edition, how much a person can lift or carry is based on the character's Strength, modified by the successes from a Strength + Body roll. Human Strength and Body attributes lie on a 1-6 scale, and the manual says that average humans have scores of 3. With the average person's STR + BOD = 6, it is possible to roll up to 6 successes to modify his base lifting amount (though very unlikely to get all 6 successes). Each success rolled adds 15 kg to the amount that can be lifted. Here is a graph of the average lifting abilities (after rolling) for characters of average Body and any given Strength:
We see here that the average real-world person is as strong as a Shadowrun character with a Strength of 2, one level below average given an average Body. The perfectly average Shadowrun character will (on an average roll) be stronger than about 70% of real people. With the randomization in the game mechanics, it is possible for characters with strength of 2 to lift more than shown on this graph about 26% of the time. So, it gets a little messy comparing the probability distributions of game characters to the single limits I have for real people. Real people just do not have wide variance for how much an individual is able to lift. A person's max lift will fluctuate a little based on factors like rest, warm-up, time of day, and how long it's been since working out, but the fluctuation will not come anywhere close to the 90 kg variance an average Shadowrun character has.
Shadowrun's mechanics have the typical trend that average characters are stronger than average real-world people, but on average the difference is not as severe as other popular systems. What is quite deviant in the mechanics is the huge variance within a single person due to rolling so many dice to determine lifting ability during each attempt to lift something.
Here is a table of probabilities of successes based on die pool:
Here is the table of base lifting amounts and modifiers:
Rolled successes add 15 kg to lifting, and 10 kg to carrying. I would prefer the system to have less randomization. It is also unfortunately messy to use the real strengths that I have in comparison to Shadowrun characters all of Body 3. I have no clear way to break real world people into six Shadowrun-equivalent groups by body size to create separate graphs by Body and Strength. This is one of the least clear comparisons I'm making for strength, but I hold to the opinion that less randomization is better in a simulation mechanic.
We see here that the average real-world person is as strong as a Shadowrun character with a Strength of 2, one level below average given an average Body. The perfectly average Shadowrun character will (on an average roll) be stronger than about 70% of real people. With the randomization in the game mechanics, it is possible for characters with strength of 2 to lift more than shown on this graph about 26% of the time. So, it gets a little messy comparing the probability distributions of game characters to the single limits I have for real people. Real people just do not have wide variance for how much an individual is able to lift. A person's max lift will fluctuate a little based on factors like rest, warm-up, time of day, and how long it's been since working out, but the fluctuation will not come anywhere close to the 90 kg variance an average Shadowrun character has.
Shadowrun's mechanics have the typical trend that average characters are stronger than average real-world people, but on average the difference is not as severe as other popular systems. What is quite deviant in the mechanics is the huge variance within a single person due to rolling so many dice to determine lifting ability during each attempt to lift something.
Here is a table of probabilities of successes based on die pool:
Here is the table of base lifting amounts and modifiers:
Rolled successes add 15 kg to lifting, and 10 kg to carrying. I would prefer the system to have less randomization. It is also unfortunately messy to use the real strengths that I have in comparison to Shadowrun characters all of Body 3. I have no clear way to break real world people into six Shadowrun-equivalent groups by body size to create separate graphs by Body and Strength. This is one of the least clear comparisons I'm making for strength, but I hold to the opinion that less randomization is better in a simulation mechanic.
Sep 17, 2011
Mutants and Masterminds - Strength and Lifting
Mutants and Masterminds is one of my favorite systems. The mechanics made excellent improvements on the d20 system. Since it uses a point-buy system, there is no real distribution of strength. Since it is based on the d20 system, though, which originally determined strength with a 3d6, I am using the 3d6 curve as a proxy of the distribution of strength within M&M.
It is accurate enough at the far bottom and top of the distribution of lifting ability, but, as with nearly every other system, it overestimates the abilities of most people in the average range. The average person in the M&M system is stronger than 75% of people in the real world. The average person in the real world is only stronger than 10% of people in the M&M system.
Here is the lifting/dragging table for M&M 2nd ed. Weights are in pounds.
It is accurate enough at the far bottom and top of the distribution of lifting ability, but, as with nearly every other system, it overestimates the abilities of most people in the average range. The average person in the M&M system is stronger than 75% of people in the real world. The average person in the real world is only stronger than 10% of people in the M&M system.
Here is the lifting/dragging table for M&M 2nd ed. Weights are in pounds.
Aug 31, 2011
I'm Not Dead
I am still gradually recovering from the loss of my last computer. I decided to try Open Office on the new one instead of buying MS Office or using my super old version, but Open Office makes my graphs uglier than they already were, so I am just going to install MS Office 2000. My workplace is no better.
This site got over 600 views in August. I've got visitors from over 30 countries. Eastern Asia is especially interested in the Principals of Recreation. Many of you are looking for probability tables for Shadowrun 4th edition and World of Darkness, and for strength and intelligence information for D&D. Many of you are also looking for the probability of death from falls of different heights, adult weight distributions, and adult deadlifting capabilities. I have very few return visitors, as most of you tend to be searching for something in particular, find it and leave.
My personal favorite posts do not turn up in people's searches, and have very few views: RPG mechanics taxonomy, determining if dice are lucky, and a taxonomy of action success probability systems.
Projects I have in mind for the future are to finish out the deadlifting series, revisit death by falls for each system individually with greater detail, interviews with RPG designers, commentary on intelligence simulation, and the most comprehensive list of possible in-game effects.
This site got over 600 views in August. I've got visitors from over 30 countries. Eastern Asia is especially interested in the Principals of Recreation. Many of you are looking for probability tables for Shadowrun 4th edition and World of Darkness, and for strength and intelligence information for D&D. Many of you are also looking for the probability of death from falls of different heights, adult weight distributions, and adult deadlifting capabilities. I have very few return visitors, as most of you tend to be searching for something in particular, find it and leave.
My personal favorite posts do not turn up in people's searches, and have very few views: RPG mechanics taxonomy, determining if dice are lucky, and a taxonomy of action success probability systems.
Projects I have in mind for the future are to finish out the deadlifting series, revisit death by falls for each system individually with greater detail, interviews with RPG designers, commentary on intelligence simulation, and the most comprehensive list of possible in-game effects.
Aug 18, 2011
Fighting and Lifting in Flight
I recently watched a particularly awful cartoon about Superman and Shazaam, and was struck by the nonsensical fighting in mid-air. Martial arts greatly depends on leverage. Punches, kicks, dodges and throws generally involve at least one foot on the ground or forward motion. RPG rules should include at least a nod to Newton's laws of motion. A flier striking someone hard enough to send him soaring away would move backwards (or spin) at great speed also, unless the strike involved an instant whole-body acceleration in the same direction as the strike. If the flier is capable of such sudden, massive acceleration, then the flier would be able to evade or roll with strikes, and may also be immune to injury from strikes by virtue of the inherent resistance to huge forces necessary to survive his own ability to accelerate.
Strength is nearly meaningless in flight. A person's strength is based on his ability to use leverage of joints and of the body against a stable surface. If the Hulk was able to very slowly levitate himself into the air, he would not be able to do so while holding a car. If Banner is able to accelerate very rapidly to great speeds, he would be able to slowly lift a car into the air, perhaps only by pressing his entire body flat underneath it. The point is that both lifting and flying are applications of force, and are not independent of each other in the air.
What systems take any of this into consideration? Aberrant does not, but does include mechanics for additional effectiveness of certain aerial and high-speed maneuvers. There is no prohibition of fliers using their full strength or martial arts ability and damage in the air.
I don't think that it is practical to have an RPG require all the math to precisely simulate fighting and lifting in flight, but I would like to at least see some general penalties or restrictions.
Strength is nearly meaningless in flight. A person's strength is based on his ability to use leverage of joints and of the body against a stable surface. If the Hulk was able to very slowly levitate himself into the air, he would not be able to do so while holding a car. If Banner is able to accelerate very rapidly to great speeds, he would be able to slowly lift a car into the air, perhaps only by pressing his entire body flat underneath it. The point is that both lifting and flying are applications of force, and are not independent of each other in the air.
What systems take any of this into consideration? Aberrant does not, but does include mechanics for additional effectiveness of certain aerial and high-speed maneuvers. There is no prohibition of fliers using their full strength or martial arts ability and damage in the air.
I don't think that it is practical to have an RPG require all the math to precisely simulate fighting and lifting in flight, but I would like to at least see some general penalties or restrictions.
Jul 26, 2011
Point-buy Systems and Character Feature Costs - Dominion as an Example
My computer's motherboard shorted out last week, so I have no access to my files for a bit.
Liberally perceived, Dominion is a simulation of medival rulers grabbing land through human influence and resource management. I've been playing quite a lot of the basic set, but only 2-player games. We have decided that a few cards are worth different amounts of money than they are supposed to cost, at least in a 2-player game.
It is nearly impossible for game designers to figure out in advance balanced relative costs for each character feature. This is especially due to the changes in utility across settings. Our home rules for Dominion are for 2-player games, and may not stand in 4-player games. Skills that are more useful in a space opera setting may be less useful in a post-apokalypse survival campaign. We rely heavily on the GM to be aware and clever with house rules to keep players happily balanced with each other.
A friend of mine suggested using an auction system in which players could bid on features for their characters. Of course, this would be easier to implement in online games than in table-top games, but the line there is blurring as online resources are increasingly used for (sometimes virtual) table-top play. If a disproportionate amount of players are choosing a particular feature for their characters, it should cost more. If a particular feature is underrepresented, it should cost less. This would help ensure a diverse gaming experience, and allow for better creativity with character development and play less fettered by the incentives present in an unbalanced point-buy system.
Liberally perceived, Dominion is a simulation of medival rulers grabbing land through human influence and resource management. I've been playing quite a lot of the basic set, but only 2-player games. We have decided that a few cards are worth different amounts of money than they are supposed to cost, at least in a 2-player game.
- Villages normally cost 3, but we say they cost 4 (really 4.5; they sell out quickly for 4, but are not as good as cards that cost 5)
- Spies normally cost 4, but we say they cost 5
- Cellars normally cost 2, but we say they cost 3
- Adventurers normally cost 5, but we say they cost 4
- Thieves normally cost 4, but we do not get them even when they are discounted because they are double-edged swords in a 2-player game that help as often as they hurt.
It is nearly impossible for game designers to figure out in advance balanced relative costs for each character feature. This is especially due to the changes in utility across settings. Our home rules for Dominion are for 2-player games, and may not stand in 4-player games. Skills that are more useful in a space opera setting may be less useful in a post-apokalypse survival campaign. We rely heavily on the GM to be aware and clever with house rules to keep players happily balanced with each other.
A friend of mine suggested using an auction system in which players could bid on features for their characters. Of course, this would be easier to implement in online games than in table-top games, but the line there is blurring as online resources are increasingly used for (sometimes virtual) table-top play. If a disproportionate amount of players are choosing a particular feature for their characters, it should cost more. If a particular feature is underrepresented, it should cost less. This would help ensure a diverse gaming experience, and allow for better creativity with character development and play less fettered by the incentives present in an unbalanced point-buy system.
Jul 16, 2011
Rifts - Strength and Lifting
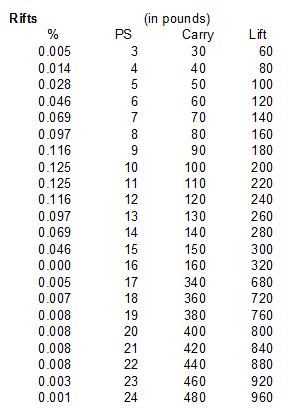
Palladium's Rifts system has a reputation for being ridiculous, but its rules for maximum lifting ability have some merit.
Since the Physical Strength (PS) attribute is randomly generated by rolling 3d6 and adding 1d6 if the sum is 16-18, the distribution is the same as D&D 3.5 up until a PS of 15, then stretches out to 24 with less than 1% of the population having each PS score from 16-24. In fact, it is impossible to have a PS of 16.
Lifting ability follows a linear progression, with a jump at PS 17 where the multiplier doubles. The game pretty accurate simulates real people at PSs 3, 14, and 15 (and 16 as projected if it were possible to roll), but way overestimates ability for average and below average people. If the multiplier did not change, and there was just one constant linear progression, the game would do a good job of simulating very strong people as well.
What is interesting to note is that the maximum amount that an unmodified human can lift in the game (960 lbs) is pretty close the maximum that any real human has lifted. It is just that the game mechanic overestimates the proportion of people who can lift that much. Perhaps far more people hit the gym really hard in the grim future of Rifts. It is important to fill up that suit of armor covered in skulls and spikes.
Here is the table of carrying and lifting ability by Physical Strength score, and the proportions of characters who would have each score by rolling.
Since the Physical Strength (PS) attribute is randomly generated by rolling 3d6 and adding 1d6 if the sum is 16-18, the distribution is the same as D&D 3.5 up until a PS of 15, then stretches out to 24 with less than 1% of the population having each PS score from 16-24. In fact, it is impossible to have a PS of 16.
Lifting ability follows a linear progression, with a jump at PS 17 where the multiplier doubles. The game pretty accurate simulates real people at PSs 3, 14, and 15 (and 16 as projected if it were possible to roll), but way overestimates ability for average and below average people. If the multiplier did not change, and there was just one constant linear progression, the game would do a good job of simulating very strong people as well.
What is interesting to note is that the maximum amount that an unmodified human can lift in the game (960 lbs) is pretty close the maximum that any real human has lifted. It is just that the game mechanic overestimates the proportion of people who can lift that much. Perhaps far more people hit the gym really hard in the grim future of Rifts. It is important to fill up that suit of armor covered in skulls and spikes.
Here is the table of carrying and lifting ability by Physical Strength score, and the proportions of characters who would have each score by rolling.
Jul 12, 2011
Dungeons and Dragons 3.5: Strength and Lifting
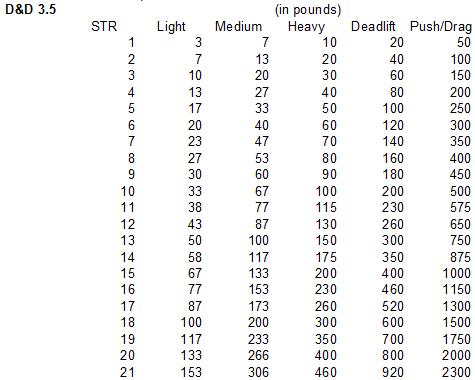
D&D 3.5, the d20 OGL line that spawned a flood of content, actually seems to have the most accurate simulation of human lifting ability. I have almost finished making graphs for the systems I have, and 3.5 looks best so far. I dislike Dungeons and Dragons in general, and this came as a surprise to me, but there you have it. It still pretty consistently overestimates people's lifting abilities, even men's by about 5-70 lbs at each score, but it has an appropriate curve.
To better simulate a real person, figure out your character's strength using the table below, then add 2 to it. For example, if you are simulating someone who can deadlift 300 pounds in real life, the table would assign the character a Strength score of 13, but a score of 15 is more appropriate based on the proportion of the population with that lifting ability. Here is the table of encumbrance thresholds for 3.5. Is this the same for Pathfinder? I do not have the Pathfinder system, but I am under the impression that it uses the same rules as 3.5.
To better simulate a real person, figure out your character's strength using the table below, then add 2 to it. For example, if you are simulating someone who can deadlift 300 pounds in real life, the table would assign the character a Strength score of 13, but a score of 15 is more appropriate based on the proportion of the population with that lifting ability. Here is the table of encumbrance thresholds for 3.5. Is this the same for Pathfinder? I do not have the Pathfinder system, but I am under the impression that it uses the same rules as 3.5.
Jul 10, 2011
Dungeons and Dragons 4th edition: Strength and Lifting
Now that I've finished creating a reasonable distribution of real human lifting ability, I can compare it to the distributions generated by the mechanics of role-playing games. Let us start with the 4th edition of Dungeons and Dragons. Here is a table showing how lifting ability is calculated in-game based on the Strength attribute:
A character holding up to a "Normal" weight does not suffer encumbrance penalties. The rules say that characters can not lift more than the "Heavy" amount, though they can still move around while holding such weight. If we go back to the roots of D&D, when Strength was determined by rolling 3d6, we could create proxy values of the proportions of the population with each Strength value (mean = 10.5). Then we can graph the amount of weight that real persons could lift along with what D&D characters can lift:
The D&D rules provide a linear progression of lifting ability. D&D 4th edition closely simulates real people's abilities at Strengths of 3 and 14-16, but gives a greater lifting ability than realistic for characters with Strengths of 4-13, and lesser for the highest human Strengths. I threw the values for real men into the graph to see if D&D was a better simulator of just men, and it does (the sum of the differences between D&D values and real values is smaller).
Of course, D&D 4th edition uses a point-buy system for attributes, so there are no clear proportions of characters with each lifting ability. Let us see what the percentiles would be of D&D characters at each Strength score if the game were an accurate simulation of real people (the 3d6 line is included just for reference):
We can see that the average D&D character should have a Strength of 6 or 7 (not 10 or 11) for the game to simulate real people. Only a quarter of characters would have Strength scores of 11 or higher.
Next up: another game's strength system gets compared to real life.
Jul 8, 2011
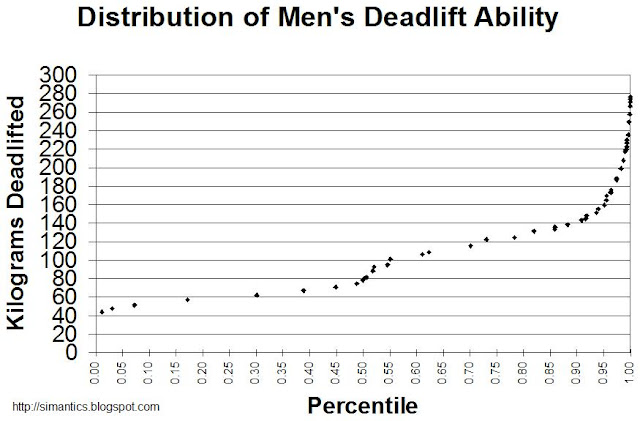
Adult Deadlifting Distribution
Here is the aggregation of men's and women's lifting abilities. Again, the graph is inaccurate for the bottom percent or so, and the estimate equation only really applies to the 5th-95th percentiles. I assumed a 52% proportion of women, not that it significantly affects the graph.
We can see a few distinct segments of data. The bottom third is pretty exclusively made up of women who do not lift weights. The middle third consists of untrained men, and women who weight train. We see a sharp upward slope around the 73rd percentile, which is due to elite women weightlifters. The 78th to 98th percentiles, roughly, are made up of men who weight train, and the spike at the end is elite weightlifting men.
Even small children and the very weakest adults can still lift at least 20 lbs. 60 lbs is a good estimate for the 5th percentile. The average adult (in the US) can lift up to 125 lbs. People in the 81st percentile can lift double the average amount. People in the 95th percentile can lift about 310 lbs. Over 400 lbs is the territory of elite men and a handful of women. Over 700 lbs is the territory of just a handful of men.
Again, there are unrealistic steps in the graph due to how the data was originally collected, and the smoother curve is probably more representative of the population. There should be a steep slope up from a low weight in the lowest few percentiles, but data is not available.
Here is the same graph in kilograms:
We can see a few distinct segments of data. The bottom third is pretty exclusively made up of women who do not lift weights. The middle third consists of untrained men, and women who weight train. We see a sharp upward slope around the 73rd percentile, which is due to elite women weightlifters. The 78th to 98th percentiles, roughly, are made up of men who weight train, and the spike at the end is elite weightlifting men.
Even small children and the very weakest adults can still lift at least 20 lbs. 60 lbs is a good estimate for the 5th percentile. The average adult (in the US) can lift up to 125 lbs. People in the 81st percentile can lift double the average amount. People in the 95th percentile can lift about 310 lbs. Over 400 lbs is the territory of elite men and a handful of women. Over 700 lbs is the territory of just a handful of men.
Again, there are unrealistic steps in the graph due to how the data was originally collected, and the smoother curve is probably more representative of the population. There should be a steep slope up from a low weight in the lowest few percentiles, but data is not available.
Here is the same graph in kilograms:
Jul 7, 2011
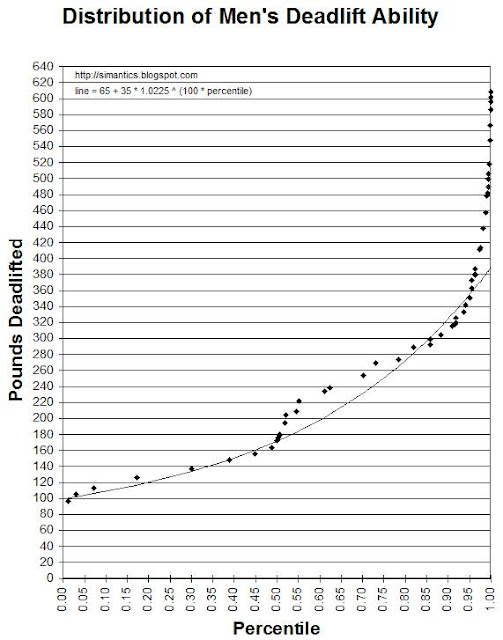
Men's Maximum Deadlifting Distribution in Pounds with Equation
I figured it would be helpful to readers to revisit the distribution for men's deadlifts using pounds instead of kilograms. Also, as I have been working on graphs for future posts, I have been tweaking equations that generate good estimates of what a person can lift at any percentile.
It is important to note that the line was not calculated to be a best-fit to the data, and that was intentional. I do not like how the deadlifting data I have creates a large jump past the 50th percentile, and it is entirely an artifact of the way the data was collected, not representative of the population, which would follow a smoother curve. The equation I settled on is 65 + 35 * 1.0225 ^ (100 * percentile) in pounds. Some day I will learn how to make equations pretty. What is it, LaTeX?
Also, the equation for the line should only be used to estimate deadlifting ability for the 5th-95th percentiles. Over the 95th, we see a sharp turn upward as the elites truly separate themselves from the pack. Below the 5th percentile, we would also see a sharp turn downward if any data had been available for unhealthy or particularly weak men. The lowest value available is the average maximum weight lifted by men with body weights in the bottom 0.005 proportion.
It is important to note that the line was not calculated to be a best-fit to the data, and that was intentional. I do not like how the deadlifting data I have creates a large jump past the 50th percentile, and it is entirely an artifact of the way the data was collected, not representative of the population, which would follow a smoother curve. The equation I settled on is 65 + 35 * 1.0225 ^ (100 * percentile) in pounds. Some day I will learn how to make equations pretty. What is it, LaTeX?
Also, the equation for the line should only be used to estimate deadlifting ability for the 5th-95th percentiles. Over the 95th, we see a sharp turn upward as the elites truly separate themselves from the pack. Below the 5th percentile, we would also see a sharp turn downward if any data had been available for unhealthy or particularly weak men. The lowest value available is the average maximum weight lifted by men with body weights in the bottom 0.005 proportion.
Jul 5, 2011
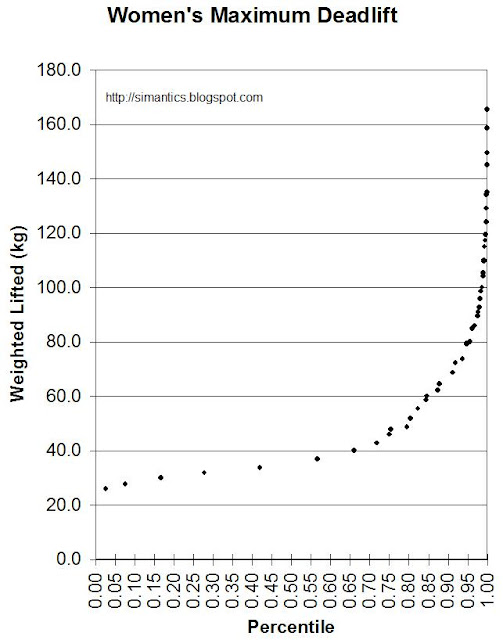
Women's Maximum Deadlifting Distribution
As I have done for men, I came up with a reasonable distribution of the lifting capabilities of US women. Global data just is not available. The proportion of women who lift weights has nearly tripled over the last two decades to 21%, but this does not tell us what proportion weight-train with the goal of really getting strong. I estimated some proportions to combine with the deadlifting table for women.
It is interesting to note that any person can almost double what they can lift with six months of diligent training. Also, the proportions of people rigorously training are fluid over time as weight-lifting fluctuates in popularity. As women's sports have become more popular, and the health benefits of weight training become more obvious with increased scientific research, the curve in these graphs has become less acute, and may continue to straighten out a little in the future. These graphs are snapshots in time, and do only apply to healthy women who have had the advantages of a first-world nation. I've got these for you in pounds and kilograms, for your convenience.
The strongest woman in the world has deadlifted 686 pounds (311 kg), so that is the current 0.000000001 level for women, and requires a life dedicated to building strength.
For some clean RPG mechanic guidelines, the average woman can lift about 80 lbs (or let's say 35 kg). A woman who is small and particularly weak should still be able to lift at least half as much. Women at the 95th percentile can lift twice as much as an average woman. The hard-training elite can lift four times the average. These ratios are very similar to those for the men, except that the strongest woman in the world lifts almost nine times the average.
Next post: all adults together, which should really be the standard for developing RPG strength scales.
It is interesting to note that any person can almost double what they can lift with six months of diligent training. Also, the proportions of people rigorously training are fluid over time as weight-lifting fluctuates in popularity. As women's sports have become more popular, and the health benefits of weight training become more obvious with increased scientific research, the curve in these graphs has become less acute, and may continue to straighten out a little in the future. These graphs are snapshots in time, and do only apply to healthy women who have had the advantages of a first-world nation. I've got these for you in pounds and kilograms, for your convenience.
The strongest woman in the world has deadlifted 686 pounds (311 kg), so that is the current 0.000000001 level for women, and requires a life dedicated to building strength.
For some clean RPG mechanic guidelines, the average woman can lift about 80 lbs (or let's say 35 kg). A woman who is small and particularly weak should still be able to lift at least half as much. Women at the 95th percentile can lift twice as much as an average woman. The hard-training elite can lift four times the average. These ratios are very similar to those for the men, except that the strongest woman in the world lifts almost nine times the average.
Next post: all adults together, which should really be the standard for developing RPG strength scales.
Jul 3, 2011
Women's and All Adult Weight Distributions
Continuing to use the EPA data, I plotted out a weight distribution for women. Unlike the men's distribution, though, women's does not have a normally distributed natural log, so I filled in missing values without an equation. The women's distribution has a more pronounced curve than men's. I then figured overall adult weights by weighting and consolodating the men's and women's distributions with the assumption that our adult population is 52% women.
This information will be useful for players of games that take weight into consideration, such as Heavy Gear and Shadowrun. Readers may want to keep in mind that people's weights peak in late middle age, and are lowest in early adulthood, with an average difference of about 15 lbs. Also, there are racial differences. Some supplementary information on racial differences (the EPA only lists Blacks and Whites) can be found here.
The next step will be to find the proportion of women who weight-train, combine their weights with the deadlifting table, and plot women's deadlifting ability distribution, as well as for all adults, as I have already done for men.
This information will be useful for players of games that take weight into consideration, such as Heavy Gear and Shadowrun. Readers may want to keep in mind that people's weights peak in late middle age, and are lowest in early adulthood, with an average difference of about 15 lbs. Also, there are racial differences. Some supplementary information on racial differences (the EPA only lists Blacks and Whites) can be found here.
Jul 1, 2011
Men's Maximum Deadlifting Distribution
Okay, still using the best source of strength data I could find, the distribution of men's body weights, and a scant article on a CDC study on the proportion of people who work out, I made a reasonable graph of the distribution of adult male maximum lifting ability.
Now, we know for a fact that there are dudes on this Earth who can lift over 400kg, but this graph only tracks up to the top 0.0001 of men. About 0.00000001 of men can lift 450kg. Also, I have no lifting data for the bottom 0.0034 of men, which should not be a big deal for RPG mechanics development.
Clearly, the average man can deadlift a max of ~80kg, or about 176 lbs. The weakest men can still lift about half that, and men at the 95th percentile can lift about double that. Elite lifters can handle three times as much as an average man, and the strongest men in the world can lift five times as much. Those are some clean, easy guidelines for simulations.
This graph is the predecessor of the top graph, and shows the same data with a different x scale:
I will eventually do this for women. Men tend to lift .42 to .64 more than women of the same body weight and same training. Since men also tend to be heavier and lift weights more often, the women's distribution is probably about half of men's.
I will also compare the strength progressions of popular RPG systems to this real distribution, and rate them by how accurately they simulate real life, as well as by playability, of course. I am using only deadlifts because nearly every system has rules for the maximum amount that a character can lift and not be able to move with, and most systems have no mechanics for other exercises.
Now, we know for a fact that there are dudes on this Earth who can lift over 400kg, but this graph only tracks up to the top 0.0001 of men. About 0.00000001 of men can lift 450kg. Also, I have no lifting data for the bottom 0.0034 of men, which should not be a big deal for RPG mechanics development.
Clearly, the average man can deadlift a max of ~80kg, or about 176 lbs. The weakest men can still lift about half that, and men at the 95th percentile can lift about double that. Elite lifters can handle three times as much as an average man, and the strongest men in the world can lift five times as much. Those are some clean, easy guidelines for simulations.
This graph is the predecessor of the top graph, and shows the same data with a different x scale:
I will eventually do this for women. Men tend to lift .42 to .64 more than women of the same body weight and same training. Since men also tend to be heavier and lift weights more often, the women's distribution is probably about half of men's.
I will also compare the strength progressions of popular RPG systems to this real distribution, and rate them by how accurately they simulate real life, as well as by playability, of course. I am using only deadlifts because nearly every system has rules for the maximum amount that a character can lift and not be able to move with, and most systems have no mechanics for other exercises.
Jun 24, 2011
Men's Body Weight Distribution
On my quest for determining how much people can lift, I developed this graph of men's body weights in pounds. The natural log of men's weights in kilograms follows a normal distribution with a standard deviation of 0.165. The equation I used, based on the EPA's data on the weights of American men ages 18-74, is e^(Standard_Deviations * 0.165 + 4.34) in kilograms. The proportion of men of each weight is in percent.
Some RPG systems have rules regarding character weight. For example, Heavy Gear and Shadowrun 4th ed. have attributes for Size or Body, respectively, based on the size of a person's body. In real life, for the purposes of determining strength, the maximum amount of weight that a man can lift is close to 3.5 times his weight. D&D is ridiculous for allowing halflings to have a STR of 18 at creation.
Some RPG systems have rules regarding character weight. For example, Heavy Gear and Shadowrun 4th ed. have attributes for Size or Body, respectively, based on the size of a person's body. In real life, for the purposes of determining strength, the maximum amount of weight that a man can lift is close to 3.5 times his weight. D&D is ridiculous for allowing halflings to have a STR of 18 at creation.
Jun 23, 2011
Strength and Untrained Lifting in Aberrant
I am crunching data on human strength for a series of posts on how TTRPGs model it. This post can be written early as a teaser because White Wolf's Aberrant rules separate out lifting capacity by untrained natural ability and the product of training. Untrained strength in Aberrant has a scale from 1 to 5, with 2 being average. There is no real standard deviation for the Aberrant stats, but it seemed reasonable enough to use each ability level as a proxy.
As I will go into in more detail in a later post, the best resource I found for lifting ability shows average weight lifted for each body weight category. While trying to find distributions of adult male body weight so that I could determine the proportion of men who could lift each amount of weight, I found a couple differing sets of numbers from the EPA and WolframAlpha, and a set for older men from an organization in Cambridge, MA. The problem with weight is that it does not follow a normal distribution, so I cannot use the mean and standard deviation to calculate any value. However, the natural log (ln) of weight does, and that may help me. The differences between the data sets seem small enough not to significantly affect my work, and are at least partially explained by the general rise in Americans' weights over the last couple decades. For the graph above, the x-axis is technically mislabeled, but each standard deviation mark refers to the percentile for that z-score, so -1 SD is about the 16th percentile, 1 SD is the 84th, 2 SD is the 97.7th, and 3 SD is about the 99.9th.
As you can see, the Aberrant rules are pretty bad at simulating real untrained strength among men. When I finish figuring out what the distribution of strength is for all men, women, and adults together, I will show how each RPG system performs as a simulator, and I will revisit the Aberrant system to include the weightlifting skill.
As I will go into in more detail in a later post, the best resource I found for lifting ability shows average weight lifted for each body weight category. While trying to find distributions of adult male body weight so that I could determine the proportion of men who could lift each amount of weight, I found a couple differing sets of numbers from the EPA and WolframAlpha, and a set for older men from an organization in Cambridge, MA. The problem with weight is that it does not follow a normal distribution, so I cannot use the mean and standard deviation to calculate any value. However, the natural log (ln) of weight does, and that may help me. The differences between the data sets seem small enough not to significantly affect my work, and are at least partially explained by the general rise in Americans' weights over the last couple decades. For the graph above, the x-axis is technically mislabeled, but each standard deviation mark refers to the percentile for that z-score, so -1 SD is about the 16th percentile, 1 SD is the 84th, 2 SD is the 97.7th, and 3 SD is about the 99.9th.
As you can see, the Aberrant rules are pretty bad at simulating real untrained strength among men. When I finish figuring out what the distribution of strength is for all men, women, and adults together, I will show how each RPG system performs as a simulator, and I will revisit the Aberrant system to include the weightlifting skill.
Jun 19, 2011
19 Principles of Recreation
These are Nineteen Principles of recreation from Howard Braucher, Secretary of the National Recreation Association in the mid-1930s. I took these from Charles Smith's book, which I posted about here and here. They are quite applicable to the children and adults of today, though there are new forms of recreation available today. As you read, pretend that "man" means "adult". Emphasis is mine:
1) Every child needs to be exposed to the growth-giving activities that have brought satisfaction through the ages -- to climbing, chasing, tumbling; to tramping, swimming, dancing, skating, ball games; to singing, playing musical instruments, dramatizing; to making things with his hands, to working with sticks and stones and sand and water, to building and modeling; to caring for pets; to gardening, to nature; to trying simple scientific experiments; to learning team play, group activity and adventure, comradeship in doing things with others.
2) Every child needs to discover which activities give him personal satisfaction. In these activities he should be helped to develop the essential skills. Several of these activities should be of such a nature that he can keep them up in adult life.
3) Every man should have certain forms of recreation which require little space and which can be fitted into small fragments of time.
4) Every man needs to know well a certain limited number of indoor and outdoor games which he himself likes so that there will never be an occasion when he cannot think of anything to do.
5) Every man should be helped to form the habit of finding pleasure in reading.
6) Most men should know at least a few songs with good music so that they may sing when they feel like it.
7) Every man should be helped to learn how to make something of beauty in line, form, color, sound, or graceful use of his own body. At least he should find pleasre in what others do in painting, woodworking, sculpture, photography, if he cannot himself use these forms of expression.
8) Every man should be helped to form habits of being active, of breathing deeply in the sunlit outdoor air. Man thrives best in the sunlight. Since living, not business, is the end of life, our cities should be planned for living as well as for business and industry. Sunlight, air, open spaces, parks, playgrounds, in abundant measure are essentials to any living that is to give permanent satisfaction.
9) Every man should be encouraged to find one or more hobbies.
10) It is of the greatest importance that every person be exposed to rhythm bcause without rhythm man is incomplete.
11) About one year in every ten of a man's life is spent in eating. It is of fundamental importance that this one-tenth of a man's life shall be so lit up by play of mind upon mind that eating shall not be a hurried chore but an oppourunity for comradeship and for growth for the whole man. Eating should be a social occasion, in the home something of a ceremony.
12) Rest, repose, reflection, contemplation are in themselves a form of recreation and ought never to be crowded out by more active play.
13) Those recreation activities are most important which most completely command the individual so that he loses himself in them and gives all that he has and is to them.
14) Ultimate satisfaction in recreation comes only through one's own achievement of some kind.
15) The form of one's recreation as an adult, often, though not always, should be such as to use in part powers unused in the rest of one's life.
16) A man is successful in his recreation life in so far as the forms of activity he chooses create a play spirit, a humor, which to some extent pervades all his working hours, helping him to find enjoyment constantly in the little events of life.
17) The happy play of childhood is essential to normal growth. Normal men are most likely to grow from the children who have played well and happily. Normal men more easily continue normally as they keep up childhood habits of play.
18) Participation as a citizen in the cooperative building of a better way of life in which all may share is one of the most permanently satisfying forms of recreation.
19) That children and men and women may be more likely to live this kind of life, experience shows there is need for community action:
The message I get from these principles in regards to role-playing games as they exist today are that RPGs are a great form of recreation for children and adults, but clearly should not be the sole form of a person's recreation. Engage in live-action role-play. There is joy in creation, storytelling, and community.
1) Every child needs to be exposed to the growth-giving activities that have brought satisfaction through the ages -- to climbing, chasing, tumbling; to tramping, swimming, dancing, skating, ball games; to singing, playing musical instruments, dramatizing; to making things with his hands, to working with sticks and stones and sand and water, to building and modeling; to caring for pets; to gardening, to nature; to trying simple scientific experiments; to learning team play, group activity and adventure, comradeship in doing things with others.
2) Every child needs to discover which activities give him personal satisfaction. In these activities he should be helped to develop the essential skills. Several of these activities should be of such a nature that he can keep them up in adult life.
3) Every man should have certain forms of recreation which require little space and which can be fitted into small fragments of time.
4) Every man needs to know well a certain limited number of indoor and outdoor games which he himself likes so that there will never be an occasion when he cannot think of anything to do.
5) Every man should be helped to form the habit of finding pleasure in reading.
6) Most men should know at least a few songs with good music so that they may sing when they feel like it.
7) Every man should be helped to learn how to make something of beauty in line, form, color, sound, or graceful use of his own body. At least he should find pleasre in what others do in painting, woodworking, sculpture, photography, if he cannot himself use these forms of expression.
8) Every man should be helped to form habits of being active, of breathing deeply in the sunlit outdoor air. Man thrives best in the sunlight. Since living, not business, is the end of life, our cities should be planned for living as well as for business and industry. Sunlight, air, open spaces, parks, playgrounds, in abundant measure are essentials to any living that is to give permanent satisfaction.
9) Every man should be encouraged to find one or more hobbies.
10) It is of the greatest importance that every person be exposed to rhythm bcause without rhythm man is incomplete.
11) About one year in every ten of a man's life is spent in eating. It is of fundamental importance that this one-tenth of a man's life shall be so lit up by play of mind upon mind that eating shall not be a hurried chore but an oppourunity for comradeship and for growth for the whole man. Eating should be a social occasion, in the home something of a ceremony.
12) Rest, repose, reflection, contemplation are in themselves a form of recreation and ought never to be crowded out by more active play.
13) Those recreation activities are most important which most completely command the individual so that he loses himself in them and gives all that he has and is to them.
14) Ultimate satisfaction in recreation comes only through one's own achievement of some kind.
15) The form of one's recreation as an adult, often, though not always, should be such as to use in part powers unused in the rest of one's life.
16) A man is successful in his recreation life in so far as the forms of activity he chooses create a play spirit, a humor, which to some extent pervades all his working hours, helping him to find enjoyment constantly in the little events of life.
17) The happy play of childhood is essential to normal growth. Normal men are most likely to grow from the children who have played well and happily. Normal men more easily continue normally as they keep up childhood habits of play.
18) Participation as a citizen in the cooperative building of a better way of life in which all may share is one of the most permanently satisfying forms of recreation.
19) That children and men and women may be more likely to live this kind of life, experience shows there is need for community action:
- Every community needs a person, and an unpaid committee or board charged with thinking, planning, and working to provide opportunity for the best possible use of the leisure hours of men, women, and children.
- Community recreaion programs should continue throughout the year
- Support of community recreation proams should be through tax funds under some dpartment of the local government.
- Every community needs playgounds, parks, and recreation centers just as every city and town needs streets and sewers.
- Every community should provide opportunity for the children when they leave school to continue the musical and dramatic and other specialized recreation activities which they have enjoyed during school days.
- Community recreation progams should allow for a broad range of tastes and interests and varying degrees of mental and physical energy.
- Every community needs persons trained to lead in recreation just as much as it needs persons trained in education.
- Satisfying recreation, whether for the individual or for the community, involves careful planning.
The message I get from these principles in regards to role-playing games as they exist today are that RPGs are a great form of recreation for children and adults, but clearly should not be the sole form of a person's recreation. Engage in live-action role-play. There is joy in creation, storytelling, and community.
Jun 16, 2011
Game Mastering: Old School Advice from Charles F. Smith part 2
This is the continuation of my presentation of Charles Smith's almost 80-year old advice on running games for groups. Part 1 is here.
Expect the Best. The text describes progressive mastery of gradually harder tasks, or learning desirable tasks that are similar to the possibly undesireable behaviors that kids will engage in on their own. For applicability to simulation games, this reminds me of gradually introducing more complicated rules as players master basic rules (especially games like Advanced Squad Leader). I'm drawing a blank on the second part.
Discipline Positively. Be a "cheery suggester" rather than a "dominating director." "When problems arise our first tendency is to blame the other fellow, but if we ask ourselves first, 'Is there anything wrong with my leadership?' second, 'Is the author to blame for suggesting such a game?' and finally, 'Is anything wrong with the players?' we must admit that the players are usually doing their best. When children find pleasure in tormenting or disobeying, the leader should try to discover his own deficiencies. usually players have well founded reasons for unusual conduct or lack of cooperation. A successful leader can secure attention by merely asking for it and refusing to talk until he gets it. He makes the group feel that the individual annoying the leader is transgressing against the group rather than against the leader." There's a great big quote for GMing. This philosophy is an explicit part of leadership positions in Battlemaster.
Change Plans. Situations change, and you should have a wide enough repetoire of options that you can adapt to unforeseen circumstances. Don't railroad your players. Players will come up with all sorts of plans and actions that don't fit your preparations, and the games will be much more fun and rewarding if you can roll with them.
Provide "Re-creation," Avoid "Wreck-Creation." "The physical well-being and happiness of the people in a leader's charge should be his first consideration." Kids need rest breaks. Players need breaks too, but I've never known this to be a problem.
Develop Athletic Girls. Physical games are great for girls up to age 12 or 14, just the same as boys. Hey, role-playing games are great for girls of all ages.
Know Your People. Offer games that the kids will actually like to play (different ages have different abilities and preferences). This should be a no-brainer. You will not have much of a game if you try to run games your friends do not want to play.
Consider Outside Interests. People like variety in addition to things that they are good at. My paraphrasing of Smith's writing in this section does not really match the header, but both are good to keep in mind. Games can integrate the varied interests of your players, as well as expose them to new topics they may enjoy.
Provide for All. Avoid games in which losers drop out. Dodge Ball is a horrible game because the kids who need most to develop skills are excluded early on and sit around. For RPGs I think this translates into avoiding games in which characters can permanently die. This is controversial, and your group is probably able to decide whether they want that or not, but especially new players may not accurately predict how they would be affected by permanent character death.
Consider the Place. Don't have city kids play soccer near a forest because they will just want to play hunting/seeking/exploring types of games. This may be another non-issue. I've never known this to be a problem. Gaming groups are generally good about coming together to play the game, and not to get distracted.
Next up: 19 principles of recreation from Howard Braucher, Secretary of the National Recreation Association in the mid-1930s. Then I'll get back to the math and simulation mechanics.
Expect the Best. The text describes progressive mastery of gradually harder tasks, or learning desirable tasks that are similar to the possibly undesireable behaviors that kids will engage in on their own. For applicability to simulation games, this reminds me of gradually introducing more complicated rules as players master basic rules (especially games like Advanced Squad Leader). I'm drawing a blank on the second part.
Discipline Positively. Be a "cheery suggester" rather than a "dominating director." "When problems arise our first tendency is to blame the other fellow, but if we ask ourselves first, 'Is there anything wrong with my leadership?' second, 'Is the author to blame for suggesting such a game?' and finally, 'Is anything wrong with the players?' we must admit that the players are usually doing their best. When children find pleasure in tormenting or disobeying, the leader should try to discover his own deficiencies. usually players have well founded reasons for unusual conduct or lack of cooperation. A successful leader can secure attention by merely asking for it and refusing to talk until he gets it. He makes the group feel that the individual annoying the leader is transgressing against the group rather than against the leader." There's a great big quote for GMing. This philosophy is an explicit part of leadership positions in Battlemaster.
Change Plans. Situations change, and you should have a wide enough repetoire of options that you can adapt to unforeseen circumstances. Don't railroad your players. Players will come up with all sorts of plans and actions that don't fit your preparations, and the games will be much more fun and rewarding if you can roll with them.
Provide "Re-creation," Avoid "Wreck-Creation." "The physical well-being and happiness of the people in a leader's charge should be his first consideration." Kids need rest breaks. Players need breaks too, but I've never known this to be a problem.
Develop Athletic Girls. Physical games are great for girls up to age 12 or 14, just the same as boys. Hey, role-playing games are great for girls of all ages.
Know Your People. Offer games that the kids will actually like to play (different ages have different abilities and preferences). This should be a no-brainer. You will not have much of a game if you try to run games your friends do not want to play.
Consider Outside Interests. People like variety in addition to things that they are good at. My paraphrasing of Smith's writing in this section does not really match the header, but both are good to keep in mind. Games can integrate the varied interests of your players, as well as expose them to new topics they may enjoy.
Provide for All. Avoid games in which losers drop out. Dodge Ball is a horrible game because the kids who need most to develop skills are excluded early on and sit around. For RPGs I think this translates into avoiding games in which characters can permanently die. This is controversial, and your group is probably able to decide whether they want that or not, but especially new players may not accurately predict how they would be affected by permanent character death.
Consider the Place. Don't have city kids play soccer near a forest because they will just want to play hunting/seeking/exploring types of games. This may be another non-issue. I've never known this to be a problem. Gaming groups are generally good about coming together to play the game, and not to get distracted.
Next up: 19 principles of recreation from Howard Braucher, Secretary of the National Recreation Association in the mid-1930s. Then I'll get back to the math and simulation mechanics.
Jun 13, 2011
Game Mastering: Old School Advice from Charles F. Smith part 1
I had the great fortune to come across a copy of Games and Game Leadership by Charles F. Smith (the 1949 13th ed; the first was published in 1933). Though it mostly refers to group games of physical activity for children, many of the principles apply to running table-top role-playing games (and parenting). Professor Smith taught a university course on the topic for many years. Here are some excerpts (in quotes), paraphrases, and notes (in italics) on how they may apply to modern RPG game mastering (dungeon mastering, storytelling, whathaveyou). Some of these do not apply very well, but I include them for interest.
Be Enthusiastic. Enthusiasm is contagious. Enjoy your work. An enthusiastic GM may have an easier time engaging the interests of players, and have a lower chance of burnout.
Develop a Sense of Humor. Be human and share in the fun of the tasks rather than being a dictator. If your players are engaging in a lot of humorous table talk instead of focusing seriously on the game, accept that that's what they're enjoying and roll with it.
Overlook Mistakes. Be sympathetic and understanding. "The person who makes he mistake invariably feels worse for having erred than any one else. If he blunders due to lack of skill, the leader should help him to develop the necessary skill. Every one who participates in athletics appreciates the coach who subtly points out errors in a general way rather than one who constantly finds fault with the individual members of the team." If someone gets a significant rule or mechanic wrong, you can remind the table of the rule while being considerate of the player's feelings.
Anticipate Blunders. Anticpate common blunders and check them without interrupting the game (like the rafting instructors blocking the bad routes on the river). "Individual reprimands are warranted only when the act in question threatens the moral growth of the entire group." Maybe put some bookmarks in your rulebook or photocopy frequently referenced rules or tables to help people play quickly and accurately. Scold people who seem to be bending rules on purpose.
Be Lenient. Do not nag. Let the kids have fun and not play in an exact way (but they still have to follow the rules.) Rules may be less important to follow in an RPG. Charles was mostly writing from the perspective of adults teaching games to kids.
Develop Confidence Through Preparadness. "Confidence is acquired through experience, but even the experienced leader enjoys such confidence only when he is thoroughly prepared to do the particular
work at hand.... He sees ways for improving both the game and his leadership and is able to say the right thing at the right time, in order to create either the desired moral effect or happy morale. ...the way to win respect is to be prepared, even refer to notes if necessary." Be prepared, that's the Boy Scouts' marching song....
Guard Against Overconfidence. You don't know everything. Invite suggestions as to new ways of playing old games or to draw assistants to your confidence in the making or executing of your plans. Don't pretend to be perfect, it just makes you look foolish. I have greatly enjoyed running a huge game with a couple assistants, and I have enjoyed being a player in a game in which the players' input was solicited and used. Not only is humility a great virtue, games are easier to run and more fun for the players when the GM accepts input and help.
Conquer Trying Situations. Maintain poise, striving always at least to appear at ease when vexatious situations arise. "Avoid petty squabbles." Stay calm. This is good advice all the time. Be cool.
Adopt a Positive Attitude. The descriptive text indicates that this means Be Decisive in modern English. Make the decisions instead of deferring authority to someone else. The GM makes the rules calls. The GM's word is law. I'm in favor of a One Appeal rule, but after the appeal the matter is settled. Be assertive without being aggressive. Be clear and firm. Don't let a friend or overbearing player make rules calls for you.
Lead Just Enough. "Lead just enough to set the pattern without crushing the initiative of the players." Children need experience with self-direction under supervision since they are not always supervised. Don't railroad your players.
That's enough for part 1. I've got a few more for part 2, then a follow-up post or two from another section of the book. Good stuff.
Be Enthusiastic. Enthusiasm is contagious. Enjoy your work. An enthusiastic GM may have an easier time engaging the interests of players, and have a lower chance of burnout.
Develop a Sense of Humor. Be human and share in the fun of the tasks rather than being a dictator. If your players are engaging in a lot of humorous table talk instead of focusing seriously on the game, accept that that's what they're enjoying and roll with it.
Overlook Mistakes. Be sympathetic and understanding. "The person who makes he mistake invariably feels worse for having erred than any one else. If he blunders due to lack of skill, the leader should help him to develop the necessary skill. Every one who participates in athletics appreciates the coach who subtly points out errors in a general way rather than one who constantly finds fault with the individual members of the team." If someone gets a significant rule or mechanic wrong, you can remind the table of the rule while being considerate of the player's feelings.
Anticipate Blunders. Anticpate common blunders and check them without interrupting the game (like the rafting instructors blocking the bad routes on the river). "Individual reprimands are warranted only when the act in question threatens the moral growth of the entire group." Maybe put some bookmarks in your rulebook or photocopy frequently referenced rules or tables to help people play quickly and accurately. Scold people who seem to be bending rules on purpose.
Be Lenient. Do not nag. Let the kids have fun and not play in an exact way (but they still have to follow the rules.) Rules may be less important to follow in an RPG. Charles was mostly writing from the perspective of adults teaching games to kids.
Develop Confidence Through Preparadness. "Confidence is acquired through experience, but even the experienced leader enjoys such confidence only when he is thoroughly prepared to do the particular
work at hand.... He sees ways for improving both the game and his leadership and is able to say the right thing at the right time, in order to create either the desired moral effect or happy morale. ...the way to win respect is to be prepared, even refer to notes if necessary." Be prepared, that's the Boy Scouts' marching song....
Guard Against Overconfidence. You don't know everything. Invite suggestions as to new ways of playing old games or to draw assistants to your confidence in the making or executing of your plans. Don't pretend to be perfect, it just makes you look foolish. I have greatly enjoyed running a huge game with a couple assistants, and I have enjoyed being a player in a game in which the players' input was solicited and used. Not only is humility a great virtue, games are easier to run and more fun for the players when the GM accepts input and help.
Conquer Trying Situations. Maintain poise, striving always at least to appear at ease when vexatious situations arise. "Avoid petty squabbles." Stay calm. This is good advice all the time. Be cool.
Adopt a Positive Attitude. The descriptive text indicates that this means Be Decisive in modern English. Make the decisions instead of deferring authority to someone else. The GM makes the rules calls. The GM's word is law. I'm in favor of a One Appeal rule, but after the appeal the matter is settled. Be assertive without being aggressive. Be clear and firm. Don't let a friend or overbearing player make rules calls for you.
Lead Just Enough. "Lead just enough to set the pattern without crushing the initiative of the players." Children need experience with self-direction under supervision since they are not always supervised. Don't railroad your players.
That's enough for part 1. I've got a few more for part 2, then a follow-up post or two from another section of the book. Good stuff.
Jun 10, 2011
Side Note
I finally gave GURPS 4th edition a perusal, and I was really impressed. It looks like it fixes some of the bigger problems I had with 3rd edition. I am happy to see that point costs for HT and ST have been decreased to reflect their in-game utility relative to DX and IQ. Also, point costs for changing these four attributes have been made linear, which gets rid of the weird bump in 3rd ed. and looks prettier, though I will not go so far as to say a linear cost progression is necessarily the right way to go. Since probabilities of success follow a nice normal curve, we see decreasing returns on investment either way, but less severely with the linear costs.
I am also a big fan of many powers being turned into "advantages", and the wide variety of modifiers available to customize how the powers work and how much they cost. I haven't taken the system for a ride yet, but it looks good.
The main downside is how bulky it is. Well, maybe it's an upside. My impulse is to say that players should make characters by first thinking up a detailed character concept, then going through the books from the beginning writing down what that character would cost, then selecting deleting that go over the point limit for the campaign, or enhancing what's there if the limit has not been reached. There's way too much to memorize or keep in mind to make quick characters, but likewise it is far harder than other systems to game. It is less obvious how to make characters that are uniformly better than others for the same points. I'll keep poking at it over time.
Now that I've got falling deaths out of my system, I'm thinking of working on analyses and guides for strength scales or movement speeds. I've got some good numbers hanging around, but not as much time as I'd like.
I am also a big fan of many powers being turned into "advantages", and the wide variety of modifiers available to customize how the powers work and how much they cost. I haven't taken the system for a ride yet, but it looks good.
The main downside is how bulky it is. Well, maybe it's an upside. My impulse is to say that players should make characters by first thinking up a detailed character concept, then going through the books from the beginning writing down what that character would cost, then selecting deleting that go over the point limit for the campaign, or enhancing what's there if the limit has not been reached. There's way too much to memorize or keep in mind to make quick characters, but likewise it is far harder than other systems to game. It is less obvious how to make characters that are uniformly better than others for the same points. I'll keep poking at it over time.
Now that I've got falling deaths out of my system, I'm thinking of working on analyses and guides for strength scales or movement speeds. I've got some good numbers hanging around, but not as much time as I'd like.
Jun 5, 2011
Death by Falling: Revisions and Simulation
One thing I realized while looking over my last post was that I only showed chance of death by impact velocity, not by distance. Of course, you could calculate distances yourself, but I want to be more helpful than that (see second graph below). Also, I've been bothered by my assumption of how many meters tall a "floor" is. I had originally used the average height of the Empire State Building (12' per floor), but later used 3.5m. This morning I checked out a resource for average floor heights by building type, and used those numbers instead, assuming that Ramos's and Delany's data was mostly from residential buildings. Here is the revised graph of probabilities of death by impact velocity:
Here is the graph that I have put together from my estimates for chance of death for an average person by distance fallen, as well as two possible dice systems for simulation:
So, for a 3d6 system, you would try to roll higher than or equal to (meters_fallen - 9). For a 3d10 system, just roll higher than or equal to the number of meters fallen. For elderly characters, maybe add 2 to the number of meters fallen, or multiply by 1.5. For children or acrobats, maybe subtract 1 from meters fallen, or multiply meters by .8. Remember that even survivors are typically severely injured, even from falls of as little as 3m, and can require extensive medical treatment.
Here is the graph that I have put together from my estimates for chance of death for an average person by distance fallen, as well as two possible dice systems for simulation:
So, for a 3d6 system, you would try to roll higher than or equal to (meters_fallen - 9). For a 3d10 system, just roll higher than or equal to the number of meters fallen. For elderly characters, maybe add 2 to the number of meters fallen, or multiply by 1.5. For children or acrobats, maybe subtract 1 from meters fallen, or multiply meters by .8. Remember that even survivors are typically severely injured, even from falls of as little as 3m, and can require extensive medical treatment.
Jun 4, 2011
Death by Falling: Real World Information to Guide Mechanics Development
So I don't turn away too many readers with the length of this post, here is the executive summary:
For an average person in the real world:
My Process:
To help game designers (and for myself) with developing simulation mechanics for falling fatalities, I tried to get some real world data on fatalities and injuries from falls. My first stops, of course, were the Center for Disease Control and Prevention (CDC, because it tracks all causes of death), the National Institute of Health, and the Occupational Safety and Health Administration (OSHA, part of the Dept. of Labor). Amazingly, none of these sources made available the proportions of falls that result in fatalities or injuries by distances fallen. There was just a lot of information on the numbers of people who died from falls each year by profession, age, job, and fall context (ladder, roof, scaffold, etc...) In fact, I could only find one document via the CDC reporting a proportion of falls resulting in injuries, and it was only for Americans over the age of 65 in 2006.
I turned to regular Google searches and found a few research articles from over the last four decades with some data on fall fatalities. I also explored some information on pedestrians and unbelted drivers in front-on car collisions in case I would have to use it as a not-ideal proxy for a person hitting the ground (like the Marvel system's use of charging attack mechanics). Interestingly, the fatal car collision speeds are very close to the fatal fall speeds that I found, despite significant situational differences such as body position and impact angles. People tend to survive slightly higher speed impacts in front-on car collisions than falling.
In this graph, falling speed is estimated based on distance fallen, which was also estimated because Ramos & Delany (1986) only reported distance fallen in floors (like the Marvel system). The rest of the data points are generated by the regression equations from the Richards (2010) document, which is why the curves are so smooth.
[I later revised this graph using different assumptions about floor heights.]
Terminal Velocity:
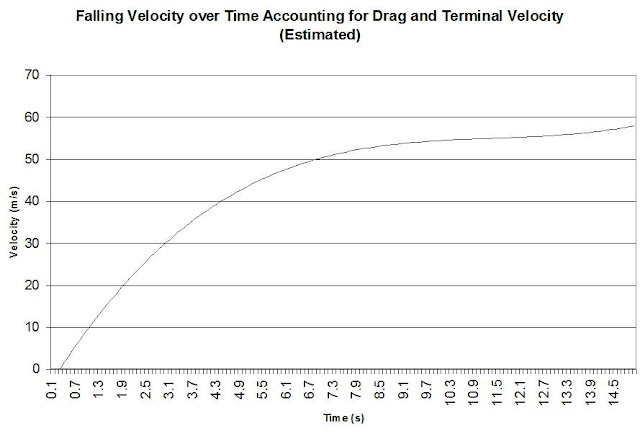
I learned a lot about terminal velocity, and made a calculator in Excel that works for dry air. Humidity and water vapor decrease air density, but I do not know how much. For an average spread man, terminal velocity is about 56 m/s near sea level.
g = gravity (9.81 m/s at sea level)
p = air density, which equals 1.225*0.9883^(altitude_in_meters_over_sea_level/80)
a = object surface area facing down, generally .5-.6 square meters for a spread skydiver
d = drag coefficient, which is probably .6 for a person (McIlveen, 2002)
I derived the equation for air density based on other information I found, so it may not be precise. Terminal velocity is largely irrelevant because 99% fatality rates occur at about .6 of terminal velocity at sea level. Using v=at works well enough up to the nearly assured fatality point that I do not feel pressured to accurately model how drag affects falling acceleration. Wikipedia says that half of terminal V is reached in about 3 seconds, which matches v=at, but that .99 of terminal V takes 15 seconds instead of <6s. This equation relatively closely approximates velocity in m/s as a function of time (s) for a 70kg person falling near sea level: y = 0.0375 x^3 + -1.28 x^2 + 14.9x + -4.02. [Edit: I do not like how the line starts at a positive value and tilts up anti-asymptotically at the end, so I would probably replace x in the equation with (x-0.35), and say that terminal velocity is fully reached at 12 seconds.]
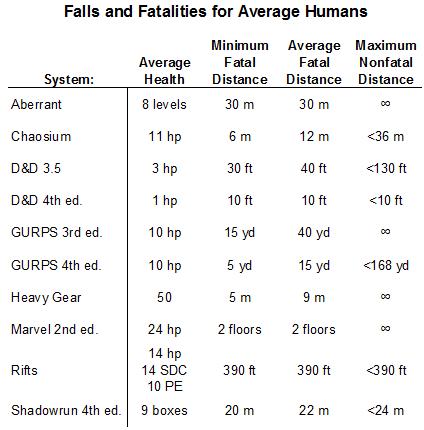
Facts:
Falls are one of the leading causes of injury and death, especially for kids and the elderly. Kids take less damage, and the elderly take a lot more. Falls are the 2nd leading cause of death for Americans age 60-72. About a quarter of elderly falls (from standing, steps, or furniture) result in injuries, and 1% of those result in death. 20-30% of elderly falls result in permanent debilitation.
Fatalities in the data here occur up to months after the falls. I do not have real data on instant deaths.
The average survived work-related fall results in 100 days of missed work. These falls are generally among contractors and roofers, from ladders, scaffolding, and roofs.
20-30% of fatal falls at work are not from a height! Tripping can be fatal if the head is struck against something in a bad way.
The record speed of falling is 614 mph, achieved over 40 years ago by a guy who jumped from a balloon at 30,000 meters where the air is only 0.015 as dense as it is at sea level.
Jumps from the Golden Gate Bridge, about 70m, have a 2% survival rate, but even many who survive the fall drown quickly. 80% break bones, mostly ribs, and 75% suffer lung injuries. More than half rupture their livers, and a quarter fracture their skulls. The record high dive is from about 52m (you can find videos on YouTube). It is vital to hit the water feet first, minimizing surface area and protecting the torso and head.
The Richards document for the London DfT has a great graph on injury severities by velocity.
Sources:
Center for Disease Control and Prevention. (2008). Self-Reported Falls and Fall-Related Injuries Among Persons Aged >65 Years --- United States, 2006. MMWR, 57(09), March 7, p. 225-229.
McIlveen, J. (2002). The everyday effects of wind drag on people. Weather, 57, p. 410-413.
Occupational Safety and Health Administration, Department of Labor. (2010). 29 CFR Part 1910. Federal Register 75 (99), May 24.
Ramos, S. and Delany, H. (1986). Free falls from heights: a persistent urban problem. Journal of the National Medical Association, 78 (2), p. 111-115.
Richards, D. (2010). Road Safety Web Publication No.16: Relationship between Speed and Risk of Fatal Injury: Pedestrians and Car Occupants. Department for Transport: London.
Snyder, R. and Snow, C. (1967). Fatal injuries resulting from extreme water impact. Aerospace Medicine. 38 (8).
For an average person in the real world:
- The shortest fall distance that can result in death: 0m (or I guess ~1m if we focus on center mass)
- The average distance that will result in death: ~15m
- The maximum distance a person can fall and survive: technically any with a lot of luck and medical attention, but practically closer to 30m (still with luck and medical attention)
My Process:
To help game designers (and for myself) with developing simulation mechanics for falling fatalities, I tried to get some real world data on fatalities and injuries from falls. My first stops, of course, were the Center for Disease Control and Prevention (CDC, because it tracks all causes of death), the National Institute of Health, and the Occupational Safety and Health Administration (OSHA, part of the Dept. of Labor). Amazingly, none of these sources made available the proportions of falls that result in fatalities or injuries by distances fallen. There was just a lot of information on the numbers of people who died from falls each year by profession, age, job, and fall context (ladder, roof, scaffold, etc...) In fact, I could only find one document via the CDC reporting a proportion of falls resulting in injuries, and it was only for Americans over the age of 65 in 2006.
I turned to regular Google searches and found a few research articles from over the last four decades with some data on fall fatalities. I also explored some information on pedestrians and unbelted drivers in front-on car collisions in case I would have to use it as a not-ideal proxy for a person hitting the ground (like the Marvel system's use of charging attack mechanics). Interestingly, the fatal car collision speeds are very close to the fatal fall speeds that I found, despite significant situational differences such as body position and impact angles. People tend to survive slightly higher speed impacts in front-on car collisions than falling.
In this graph, falling speed is estimated based on distance fallen, which was also estimated because Ramos & Delany (1986) only reported distance fallen in floors (like the Marvel system). The rest of the data points are generated by the regression equations from the Richards (2010) document, which is why the curves are so smooth.
[I later revised this graph using different assumptions about floor heights.]
Terminal Velocity:
I learned a lot about terminal velocity, and made a calculator in Excel that works for dry air. Humidity and water vapor decrease air density, but I do not know how much. For an average spread man, terminal velocity is about 56 m/s near sea level.
Terminal Velocity = SQRT(2mg/pad)
m = mass of object in kgg = gravity (9.81 m/s at sea level)
p = air density, which equals 1.225*0.9883^(altitude_in_meters_over_sea_level/80)
a = object surface area facing down, generally .5-.6 square meters for a spread skydiver
d = drag coefficient, which is probably .6 for a person (McIlveen, 2002)
I derived the equation for air density based on other information I found, so it may not be precise. Terminal velocity is largely irrelevant because 99% fatality rates occur at about .6 of terminal velocity at sea level. Using v=at works well enough up to the nearly assured fatality point that I do not feel pressured to accurately model how drag affects falling acceleration. Wikipedia says that half of terminal V is reached in about 3 seconds, which matches v=at, but that .99 of terminal V takes 15 seconds instead of <6s. This equation relatively closely approximates velocity in m/s as a function of time (s) for a 70kg person falling near sea level: y = 0.0375 x^3 + -1.28 x^2 + 14.9x + -4.02. [Edit: I do not like how the line starts at a positive value and tilts up anti-asymptotically at the end, so I would probably replace x in the equation with (x-0.35), and say that terminal velocity is fully reached at 12 seconds.]

Facts:
Falls are one of the leading causes of injury and death, especially for kids and the elderly. Kids take less damage, and the elderly take a lot more. Falls are the 2nd leading cause of death for Americans age 60-72. About a quarter of elderly falls (from standing, steps, or furniture) result in injuries, and 1% of those result in death. 20-30% of elderly falls result in permanent debilitation.
Fatalities in the data here occur up to months after the falls. I do not have real data on instant deaths.
The average survived work-related fall results in 100 days of missed work. These falls are generally among contractors and roofers, from ladders, scaffolding, and roofs.
20-30% of fatal falls at work are not from a height! Tripping can be fatal if the head is struck against something in a bad way.
The record speed of falling is 614 mph, achieved over 40 years ago by a guy who jumped from a balloon at 30,000 meters where the air is only 0.015 as dense as it is at sea level.
Jumps from the Golden Gate Bridge, about 70m, have a 2% survival rate, but even many who survive the fall drown quickly. 80% break bones, mostly ribs, and 75% suffer lung injuries. More than half rupture their livers, and a quarter fracture their skulls. The record high dive is from about 52m (you can find videos on YouTube). It is vital to hit the water feet first, minimizing surface area and protecting the torso and head.
The Richards document for the London DfT has a great graph on injury severities by velocity.
Sources:
Center for Disease Control and Prevention. (2008). Self-Reported Falls and Fall-Related Injuries Among Persons Aged >65 Years --- United States, 2006. MMWR, 57(09), March 7, p. 225-229.
McIlveen, J. (2002). The everyday effects of wind drag on people. Weather, 57, p. 410-413.
Occupational Safety and Health Administration, Department of Labor. (2010). 29 CFR Part 1910. Federal Register 75 (99), May 24.
Ramos, S. and Delany, H. (1986). Free falls from heights: a persistent urban problem. Journal of the National Medical Association, 78 (2), p. 111-115.
Richards, D. (2010). Road Safety Web Publication No.16: Relationship between Speed and Risk of Fatal Injury: Pedestrians and Car Occupants. Department for Transport: London.
Snyder, R. and Snow, C. (1967). Fatal injuries resulting from extreme water impact. Aerospace Medicine. 38 (8).
May 25, 2011
Death by Falling
[Edit: If you're looking for real information on deaths by falls, see my next two posts here and here.]
This is the first of several posts I have planned about simulating the results of falls from elevations. Here I simply determined the minimum distance necessary to fall for an average human to die, the distance at which an average person would die on average, and the maximum distance that an average person could fall without dying for ten different systems.
As you can see, there are wide differences among systems. The grades I give are subjectively based on how each mechanic models reality and contributes to game balance.
This is the first of several posts I have planned about simulating the results of falls from elevations. Here I simply determined the minimum distance necessary to fall for an average human to die, the distance at which an average person would die on average, and the maximum distance that an average person could fall without dying for ten different systems.
As you can see, there are wide differences among systems. The grades I give are subjectively based on how each mechanic models reality and contributes to game balance.
- Aberrant: For any fall under 30 meters, even the most feeble person has a 99.6% chance of only sustaining minor injuries that will heal in a day (bashing damage). At 30 meters, damage becomes lethal and maxes out at 10 dice (an average of 4 levels of damage), with only a 1.3% chance of dying even when falling miles. F
- Chaosium: Average health is actually 12hp, not 11, but the distances are correct. 1d6 damage for each 3 meters gives us a nice distribution of injuries and chances of death up to the assured death point at 36 meters. B
- D&D 3.5 (OGL): The average human in this system has 1d4 hp, which I round up to 3, but does not die until reaching -10 hp. Most falls that are not immediately fatal will still result in wounds that may result in a person's eventual death if not stabilized, but I did not calculate that. B
- D&D 4th ed.: The most appropriate stats I found for a non-heroic person in this game were for "Human Rabble", who have 1 hp. At 1d10 damage for each 10' fallen, everybody dies from any fall of at least 10'. D
- GURPS 3rd ed.: Damage involves rolling 1d6 and subtracting a constant for each yard fallen. Since it is possible to roll the constant or less on each 1d6, it is possible to take no damage at all when falling from any height. Instant death requires 6xHealth damage in the GURPS systems. D
- GURPS 4th ed.: Now there is an equation for determining how many d6 to roll based on velocity. GURPS in one of the few systems that takes acceleration into account instead of just distance. A-
- Heavy Gear: Roll 1d6 for each meter up to 10 meters, and multiply the result by meters fallen up to 30. Remember that the Silhouette system is funky, so "result" means the highest number rolled among the dice, and additional 6s each add 1 to the first 6. It is possible (ridiculously unlikely) to roll all 1s and survive any fall. It is also possible (ridiculously unlikely) to roll all 6s and die falling 5 meters. An average person has a 40% chance of death falling 8 meters, and an 81% chance of death falling 9 meters. B-
- Marvel Super Heroes 2nd ed.: The rules as written were clearly not proofread or edited. They make absolutely no sense in the English language. On page 21 the rules say to take 1 point of damage for each floor fallen (a person would have to fall 24 floors), but also say to treat falling as a charge attack. Charge attack rules on page 27 gave me the numbers I use for this post. Using the Empire State Building for reference, I decided that a "floor" is 12 feet. F
- Rifts: People take 1 point of damage for each 10' fallen. Instant death is at -(PE+1) hp. A healthy average person will survive any fall under 390'. F
- Shadowrun 4th ed.: I did not find stats for an average human. Humans have 1-6 body points, bought up from 1 at character creation. Looking at sample characters, I figured that an average human has a body of 2. Damage from falls over 6m is about (distance+4)/2, and characters roll (Body)d6 to resist some damage. For someone with a Body of 3, the distances are 22m, 24m, 28m. C
- 7th Sea: This is a game focused on dramatic swashbuckling stories, and seems to not have rules for falls.
Labels:
Aberrant,
Chaosium,
Damage,
Death,
DnD,
Falls,
GURPS,
Health,
Heavy Gear,
Marvel,
Mechanics,
Probability,
Rifts,
Shadowrun,
Silhouette
May 9, 2011
What Systems Do I Like?
People often ask me, "Why aren't you wearing any pants?" Less often, they ask, "What is your favorite role-playing game?" That is a slightly complicated question. By which criteria do I judge RPGs? The focus of this blog is their game mechanics, but a game may be a favorite based on the quality of the setting or how much fun with friends the game creates independently of mechanics and setting. Here are the RPGs I am familiar with, and how I feel about them:
- Mutants and Masterminds: This is my favorite right now. I have been very impressed with M&M's game mechanics. It fixes nearly all of the problems I have with the d20 system (OGL 3.5). There are some opportunities to min-max and create incredible powers, but an attentive GM can easily prevent it. I love the superpower setting, but the mechanics can actually be applied to recreate most other settings. I was impressed by Green Ronin for this game, and was looking for information on the 3rd ed. at their website when I found this article by their designer of the Dragon Age TTRPG in which he agrees with my own conclusion about die rolls.
- Action!: This free system by Gold Rush Games comes with instructions on customizing it! I just stumbled upon this recently and have not played it, but it incorporates mechanics that I would use if I were creating a system. It is worth checking out.
- Aberrant: This game has some of the most broken mechanics, and the canon storyline railroads campaign plots, but I have had tons of fun playing supers in this setting with friends and watching moral and ethical dilemmas unfold.
- Vampire: the Masquerade: I LARPed (live-action role-played) this for many years with the last version of the rules and setting. I have not seen the current edition. I met a lot of people this way, though not all of them were good to meet. LARPing is a great role-playing experience, and V:tM is the easiest way to experience this because it is so widespread. It's the Dungeons & Dragons of LARP. Role-playing with 50+ people at a time is a blast, and this game fosters social and political maneuvers, shifting alliances, and secrets for a fun game. Many of the other White-Wolf LARPs (Changeling, Werewolf, Mage, Oblivion) were not as conducive. A bad storyteller will rely on sending monsters in for the player characters to fight, but good storytellers have long-term NPCs infiltrate player factions and subtly construct mysteries to be solved, complete with red-herrings and ambiguous clues that lead to both conflict and collaboration. The mechanics are not great.
- Dungeons and Dragons: This is the Microsoft of the RPG world. New gamers tend to come in with D&D because it has such a broad and deep foundation. So many people play because so many other people play, and if you want to get in on a game, it is easier to find players familiar with and owning materials for D&D. I don't like classes in games because they are too constricting, and lead to conformity instead of creativity. I don't like levels in games because they also prevent customization and realistic development. I don't like hit points in games because they are wholly unrealistic, and seem to solely exist to support the level system. D&D has classes, feats, and powers set in stone in their system so they can sell lots of books with more. What I like is the mechanics to create whatever powers are desired so that players can create whatever they want from a core book. The d20 provides a linear progression of probabilities of success. I have played each edition of D&D since the late '80s because those were the games my friends were running (and once I had the materials to play with them, I also ran a campaign), but I have not been satisfied.
- Heavy Gear: I played in one campaign about 13 years ago, and I remember it being fun, largely because of the group. The mechanics are a little weird, and encourage some min-maxing, but are relatively simple and straightforward. The setting is not totally sensible, but provides opportunities for some different styles of campaigns. You can also play a flat-out tactical mech game.
- GURPS: I only got to play GURPS once, but I've made characters in anticipation of other games I was told would happen. I like that it is generic and uses point-buys. The skill system tries well to be a good simulation, which I like, but is not great for game balance. I do not like that powers and equipment are individually determined by Steve Jackson Games instead of them also giving us a point system for creating them.
- Chaosium: I'm getting around to it.
- Shadowrun: Also, just sitting on my shelf.
- Rifts: Totally silly. Thanks, Palladium.
May 6, 2011
Lucky Dice
Do you have lucky dice? This is a slightly modified version of something I wrote a couple years ago that I think has a place here.
I have encountered more than one gamer over the years who believes that he has lucky dice. These dice are reported to roll the highest damage, the most critical hits, and generally turn the player's characters into unstoppable juggernauts. Of course, I did not notice any disproportionate numbers of good or bad rolls. I argued with these players that their perceptions were tainted by the availability heuristic and confirmation bias. When they can more easily recall rolling good numbers with certain dice, they label the dice "lucky". Then, whenever those dice roll well, they say, "See? This proves the dice are lucky!" Whenever the dice roll poorly, they say, "That was a fluke! These lucky dice usually roll well.", and fail to store the failures for future recall, feeding back into the availability heuristic. Well, there is a relatively easy way to determine if a die is lucky.
If you think you have a lucky die, record what it rolls EVERY TIME. If you believe it is lucky only in a certain situation (e.g.: "This is my saving-throw die!"), then record what it rolls every time you roll it in that situation. Do not leave out any rolls. There are no Mulligans. When you have a good amount of rolls (at least 30, but more is better), you can calculate the z-score for them, then compare that z-score to a threshold. This comparison is called a one-tailed test of proportion, and we use this specific type of comparison to test the hypothesis that your die rolls a higher (not just different) proportion of good rolls than a fair die. Though there are different ways to calculate the z-score based on how sure you want to be of the results, the following simple examples should be good enough for most of you.
The equation for z is:
z = (p - Po) / (sqrt((Po(1 - Po))/n))
The variables are:
p: the proportion of the rolls you recorded that were good (natural 20, 11 or higher, 8-10 on 1d10, etc...). p = ((# of good rolls) / (total # of rolls)).
Po: the proportion expected of fair dice (0.05 for a natural 20, 0.5 for 11 or higher on d20, 0.3 for 8-10 on d10). This should technically be written as pi subscript 0.
n: the total number of rolls you recorded
To make things easy, we will use an alpha of .05 in the examples (I explain further down). This gives us a threshold of 1.645. So, all you have to do is figure out z using the equation above (or one of the examples below), and if z > 1.645 you can claim that you may have a lucky die.
Example 1:
"My die rolls high."
Po = 0.5 (half of a fair die's rolls will be above the mean, and half below)
z = (p - 0.5) / (sqrt(0.25 / n))
Example 2:
"I roll 20s."
Po = 0.05
z = (p - 0.05) / (sqrt(0.0475 / n))
To elaborate on Example 1, let's say that I claim I have a d20 that usually rolls at least an 11, and I have countless stories of how it let my characters defeat monsters and overcome challenges. I want to prove to my naysayer friends that it really is lucky, so I write down every roll for a month. I rolled the die 100 times. 58 of the rolls were at least 11, and 42 were 10 or less. I get really excited about rubbing it in everyone's faces, but remember that there's more to do. After all, I only rolled the die 100 times, and even a fair die is likely to roll 58/100 good rolls eventually. Fair dice are only expected to roll exactly 50/50 as the number of rolls approaches infinity. So, I plug in the variables:
p = 0.58
n = 100
Po = 0.5
z = (0.58 - 0.5) / (sqrt(0.25 / 100)) = 1.600
1.600 < 1.645 (our threshold)
We should probably not be impressed that 58 of the rolls were above average. If the die had rolled 59 good rolls out of 100, z would have been 1.800. What would that mean?
This is where I need to explain about alpha. In this case, alpha is the probability that you have a fair die even if z is greater than the threshold. Usually, an alpha of 0.05 lets us feel confident enough that the effect we have observed is based on the properties of what we are observing instead of a statistical fluke of the sample of observations. It is easy to increase our confidence by using a smaller alpha, such as 0.01 (which would increase the z threshold), but using a smaller alpha increases the probability that we falsely think a lucky die is fair. There is a trade-off between the risks. Personally, I would demand a high degree of confidence, and would insist on an alpha of at most 0.01. The best way to manage both risks of false results is to get a bigger sample of rolls. So, if you want to be more sure of whether your die is lucky or not, record 200 rolls, or 500. The bigger n gets, the better.
When alpha is 0.01, the z threshold is 2.328, so even 59% good rolls does not make me confident that the die is lucky. For an alpha of 0.01, 62 out of 100 rolls would have to be above average.
To elaborate on Example 2, let's find out how many natural 20s have to be rolled with an alpha of 0.01 for someone to tell me that he rolls 20s.
(p-0.05)/(sqrt(0.0475 / 100)) > 2.328
(p-0.05)/0.0218 > 2.328
p-0.05 > .0507
p > .1007
You would have to roll 11 20s out of 100 rolls.
Good luck.
I have encountered more than one gamer over the years who believes that he has lucky dice. These dice are reported to roll the highest damage, the most critical hits, and generally turn the player's characters into unstoppable juggernauts. Of course, I did not notice any disproportionate numbers of good or bad rolls. I argued with these players that their perceptions were tainted by the availability heuristic and confirmation bias. When they can more easily recall rolling good numbers with certain dice, they label the dice "lucky". Then, whenever those dice roll well, they say, "See? This proves the dice are lucky!" Whenever the dice roll poorly, they say, "That was a fluke! These lucky dice usually roll well.", and fail to store the failures for future recall, feeding back into the availability heuristic. Well, there is a relatively easy way to determine if a die is lucky.
If you think you have a lucky die, record what it rolls EVERY TIME. If you believe it is lucky only in a certain situation (e.g.: "This is my saving-throw die!"), then record what it rolls every time you roll it in that situation. Do not leave out any rolls. There are no Mulligans. When you have a good amount of rolls (at least 30, but more is better), you can calculate the z-score for them, then compare that z-score to a threshold. This comparison is called a one-tailed test of proportion, and we use this specific type of comparison to test the hypothesis that your die rolls a higher (not just different) proportion of good rolls than a fair die. Though there are different ways to calculate the z-score based on how sure you want to be of the results, the following simple examples should be good enough for most of you.
The equation for z is:
z = (p - Po) / (sqrt((Po(1 - Po))/n))
The variables are:
p: the proportion of the rolls you recorded that were good (natural 20, 11 or higher, 8-10 on 1d10, etc...). p = ((# of good rolls) / (total # of rolls)).
Po: the proportion expected of fair dice (0.05 for a natural 20, 0.5 for 11 or higher on d20, 0.3 for 8-10 on d10). This should technically be written as pi subscript 0.
n: the total number of rolls you recorded
To make things easy, we will use an alpha of .05 in the examples (I explain further down). This gives us a threshold of 1.645. So, all you have to do is figure out z using the equation above (or one of the examples below), and if z > 1.645 you can claim that you may have a lucky die.
Example 1:
"My die rolls high."
Po = 0.5 (half of a fair die's rolls will be above the mean, and half below)
z = (p - 0.5) / (sqrt(0.25 / n))
Example 2:
"I roll 20s."
Po = 0.05
z = (p - 0.05) / (sqrt(0.0475 / n))
To elaborate on Example 1, let's say that I claim I have a d20 that usually rolls at least an 11, and I have countless stories of how it let my characters defeat monsters and overcome challenges. I want to prove to my naysayer friends that it really is lucky, so I write down every roll for a month. I rolled the die 100 times. 58 of the rolls were at least 11, and 42 were 10 or less. I get really excited about rubbing it in everyone's faces, but remember that there's more to do. After all, I only rolled the die 100 times, and even a fair die is likely to roll 58/100 good rolls eventually. Fair dice are only expected to roll exactly 50/50 as the number of rolls approaches infinity. So, I plug in the variables:
p = 0.58
n = 100
Po = 0.5
z = (0.58 - 0.5) / (sqrt(0.25 / 100)) = 1.600
1.600 < 1.645 (our threshold)
We should probably not be impressed that 58 of the rolls were above average. If the die had rolled 59 good rolls out of 100, z would have been 1.800. What would that mean?
This is where I need to explain about alpha. In this case, alpha is the probability that you have a fair die even if z is greater than the threshold. Usually, an alpha of 0.05 lets us feel confident enough that the effect we have observed is based on the properties of what we are observing instead of a statistical fluke of the sample of observations. It is easy to increase our confidence by using a smaller alpha, such as 0.01 (which would increase the z threshold), but using a smaller alpha increases the probability that we falsely think a lucky die is fair. There is a trade-off between the risks. Personally, I would demand a high degree of confidence, and would insist on an alpha of at most 0.01. The best way to manage both risks of false results is to get a bigger sample of rolls. So, if you want to be more sure of whether your die is lucky or not, record 200 rolls, or 500. The bigger n gets, the better.
When alpha is 0.01, the z threshold is 2.328, so even 59% good rolls does not make me confident that the die is lucky. For an alpha of 0.01, 62 out of 100 rolls would have to be above average.
To elaborate on Example 2, let's find out how many natural 20s have to be rolled with an alpha of 0.01 for someone to tell me that he rolls 20s.
(p-0.05)/(sqrt(0.0475 / 100)) > 2.328
(p-0.05)/0.0218 > 2.328
p-0.05 > .0507
p > .1007
You would have to roll 11 20s out of 100 rolls.
Good luck.
May 2, 2011
Graphs of Success Probability by Skill Total and Difficulty
I've given you tables of success probabilities by skill total and difficulty for two systems (World of Darkness, Shadowrun 4th ed.), plus a graph for Heavy Gear. Here I present that information again in graphs, plus two more systems, to show some of the different patterns that exist for success probabilities with increases in skill among different systems.
Linear
Here is your standard d20 system, most popular in Dungeons and Dragons. Each character has a skill modified by an attribute and various other junk, added to a d20 result and compared to a difficulty level. Each increase in the skill total raises the probability of success by 5% linearly. There is always at least a 5% chance of failure (rolling a 1). In the D&D games, skills are not bought with general character development points, but characters are alloted a few points each level to be used only for skills. Difficulty levels typically scale with character levels, so it behooves players to specialize in a few skills that are always increased with the character level in order to maintain good probabilities of success as characters level up. I am not getting in to "taking 10" or "taking 20".
Inconsistent
Here is the graph for Dream Pod 9's Silhouette system, used in their Heavy Gear game. We can see that the progression is not consistent. The lowest skill is concave, rapidly dropping the probability of success at low difficulties relative to the drop at higher difficulties where the probability of success is already very low. A skill of 1 has a linear descent. Higher skills progressively maintain high success rates among lower difficulties before rapidly plunging at higher difficulties, and then there is the bent tail as it becomes more possible to roll multiple 6s. Attribute bonuses are added to skill roll results, shifting the graph to the right without changing its shape.
Normal
Isn't that pretty? I am not sure if I am completely representing the GURPS system accurately here, but I think players just have to roll lower than the characters' skills on 3d6 to succeed at tasks (17s and 18s fail). So, there is no real "difficulty level" for tasks other than what is forced by skill levels. There may be modifiers that increase or decrease a skill for the purpose of a challenge, shifting the whole curve to the left or right. If we graphed the probabilities of each individual outcome for 3d6, the line would be shaped like a bell. I call this "normal" because as a "normal distribution" it has higher probabilities of outcomes in the middle, progressively less likely outcomes away from the middle, and is relatively symmetrical.
Inconsistent Normal
We can see here that both Shadowrun by Catalyst Game Labs and World of Darkness by White Wolf approach the normal curve as their dice pools (skill total, or skill + attribute) increase. With few dice in these systems, it is impossible to approximate the distribution of the normal pattern, and the results more follow the Inconsistent pattern. These systems both involve rolling multiple dice (d6 and d10, respectively), and counting die results over a threshold as "successes". Players need a number of successes equal to a task's difficult in order to succeed. So, the terminology can get annoying as people get a bunch of successes but still fail at a task.
I really like how the Normal distribution of probabilities of success works in simulations, but not necessarily the way that GURPS implements it in the absence of difficulty levels. In real life, when we encounter tasks far below our skill level, we are quite likely to succeed at them and have a low variance with our high success rate. When we encounter tasks far above our skill level, we are quite likely to fail at them and have a low variance with our high failure rate. Tasks closer to our skill level have increasingly variant success rates. Because of this, I am in favor of the use of normal distributions of probability of success in simulation systems. This typically requires rolling more than one die and summing the results.
Linear
Here is your standard d20 system, most popular in Dungeons and Dragons. Each character has a skill modified by an attribute and various other junk, added to a d20 result and compared to a difficulty level. Each increase in the skill total raises the probability of success by 5% linearly. There is always at least a 5% chance of failure (rolling a 1). In the D&D games, skills are not bought with general character development points, but characters are alloted a few points each level to be used only for skills. Difficulty levels typically scale with character levels, so it behooves players to specialize in a few skills that are always increased with the character level in order to maintain good probabilities of success as characters level up. I am not getting in to "taking 10" or "taking 20".
Inconsistent
Here is the graph for Dream Pod 9's Silhouette system, used in their Heavy Gear game. We can see that the progression is not consistent. The lowest skill is concave, rapidly dropping the probability of success at low difficulties relative to the drop at higher difficulties where the probability of success is already very low. A skill of 1 has a linear descent. Higher skills progressively maintain high success rates among lower difficulties before rapidly plunging at higher difficulties, and then there is the bent tail as it becomes more possible to roll multiple 6s. Attribute bonuses are added to skill roll results, shifting the graph to the right without changing its shape.
Normal
Isn't that pretty? I am not sure if I am completely representing the GURPS system accurately here, but I think players just have to roll lower than the characters' skills on 3d6 to succeed at tasks (17s and 18s fail). So, there is no real "difficulty level" for tasks other than what is forced by skill levels. There may be modifiers that increase or decrease a skill for the purpose of a challenge, shifting the whole curve to the left or right. If we graphed the probabilities of each individual outcome for 3d6, the line would be shaped like a bell. I call this "normal" because as a "normal distribution" it has higher probabilities of outcomes in the middle, progressively less likely outcomes away from the middle, and is relatively symmetrical.
Inconsistent Normal
We can see here that both Shadowrun by Catalyst Game Labs and World of Darkness by White Wolf approach the normal curve as their dice pools (skill total, or skill + attribute) increase. With few dice in these systems, it is impossible to approximate the distribution of the normal pattern, and the results more follow the Inconsistent pattern. These systems both involve rolling multiple dice (d6 and d10, respectively), and counting die results over a threshold as "successes". Players need a number of successes equal to a task's difficult in order to succeed. So, the terminology can get annoying as people get a bunch of successes but still fail at a task.
I really like how the Normal distribution of probabilities of success works in simulations, but not necessarily the way that GURPS implements it in the absence of difficulty levels. In real life, when we encounter tasks far below our skill level, we are quite likely to succeed at them and have a low variance with our high success rate. When we encounter tasks far above our skill level, we are quite likely to fail at them and have a low variance with our high failure rate. Tasks closer to our skill level have increasingly variant success rates. Because of this, I am in favor of the use of normal distributions of probability of success in simulation systems. This typically requires rolling more than one die and summing the results.
Labels:
d20,
Distribution,
DnD,
DP9,
Dream Pod 9,
Heavy Gear,
Mechanics,
Probability,
Shadowrun,
Silhouette,
System,
Taxonomy,
White Wolf,
WoD,
World of Darkness,
WW
Subscribe to:
Posts (Atom)