Point-buy Systems and Character Feature Costs - Dominion as an Example

My computer's motherboard shorted out last week, so I have no access to my files for a bit.

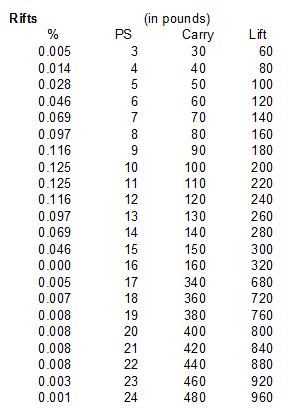
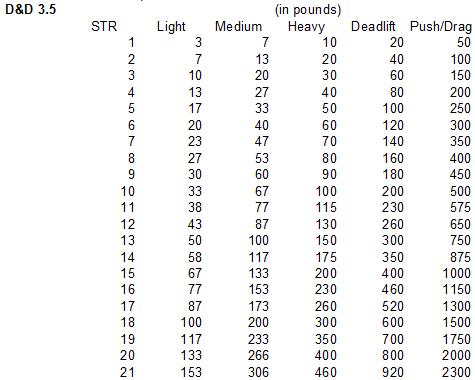
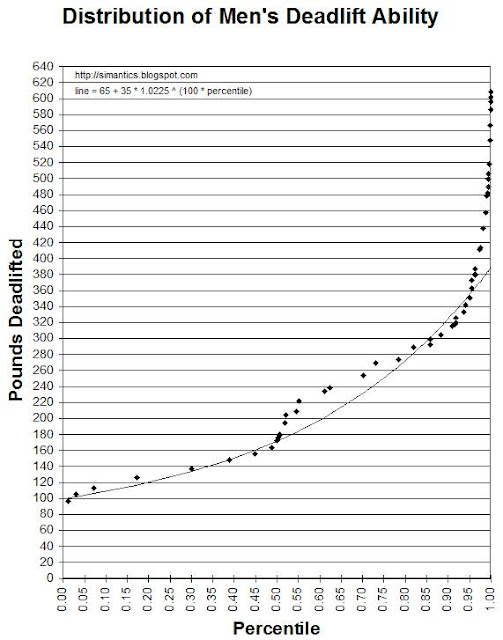
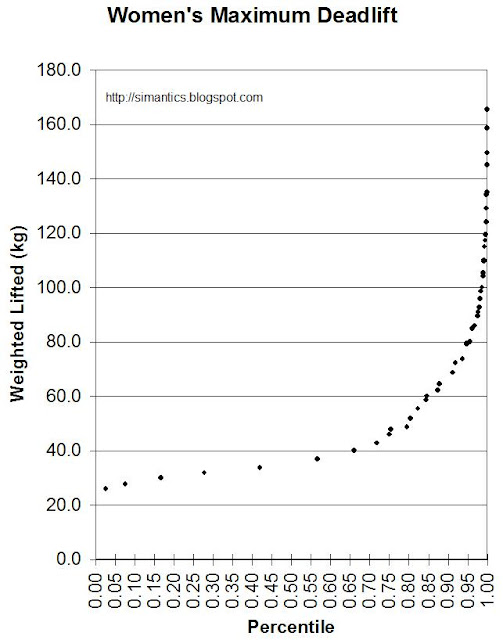
Liberally perceived, Dominion is a simulation of medival rulers grabbing land through human influence and resource management.  I've been playing quite a lot of the basic set, but only 2-player games.  We have decided that a few cards are worth different amounts of money than they are supposed to cost, at least in a 2-player game.

• Villages normally cost 3, but we say they cost 4 (really 4.5; they sell out quickly for 4, but are not as good as cards that cost 5)
• Spies normally cost 4, but we say they cost 5
• Cellars normally cost 2, but we say they cost 3
• Adventurers normally cost 5, but we say they cost 4
• Thieves normally cost 4, but we do not get them even when they are discounted because they are double-edged swords in a 2-player game that help as often as they hurt.

As we notice that a particular card is more advantageous than others of the same cost, we buy them all up.  A similar phenomenon occurs in RPGs with point-buy systems for any type of feature.  Almost no one gets Bioluminescence in Aberrant because it is terribly weak for the cost, and almost everyone wants 10 Willpower at character creation, the Adaptation Mega-Stamina enhancement, and Psychic Shield.  GURPS 4th edition fixed its point costs from 3rd edition to reflect how people responded to the comparative utilities of HT and ST to IQ and DX in game.  Since so many skills relied on IQ and DX, and nearly nothing on HT and ST, few people would spend the same number of points for levels of the latter as on the former.  Now HT and ST cost half as much.  Many skills in most systems are flat out more useful than others that cost the same to learn.

It is nearly impossible for game designers to figure out in advance balanced relative costs for each character feature.  This is especially due to the changes in utility across settings.  Our home rules for Dominion are for 2-player games, and may not stand in 4-player games.  Skills that are more useful in a space opera setting may be less useful in a post-apokalypse survival campaign.  We rely heavily on the GM to be aware and clever with house rules to keep players happily balanced with each other. 

A friend of mine suggested using an auction system in which players could bid on features for their characters.  Of course, this would be easier to implement in online games than in table-top games, but the line there is blurring as online resources are increasingly used for (sometimes virtual) table-top play.  If a disproportionate amount of players are choosing a particular feature for their characters, it should cost more.  If a particular feature is underrepresented, it should cost less.  This would help ensure a diverse gaming experience, and allow for better creativity with character development and play less fettered by the incentives present in an unbalanced point-buy system.

Rifts - Strength and Lifting

Palladium's Rifts system has a reputation for being ridiculous, but its rules for maximum lifting ability have some merit. 

 Since the Physical Strength (PS) attribute is randomly generated by rolling 3d6 and adding 1d6 if the sum is 16-18, the distribution is the same as D&D 3.5 up until a PS of 15, then stretches out to 24 with less than 1% of the population having each PS score from 16-24.  In fact, it is impossible to have a PS of 16. 

Lifting ability follows a linear progression, with a jump at PS 17 where the multiplier doubles.  The game pretty accurate simulates real people at PSs 3, 14, and 15 (and 16 as projected if it were possible to roll), but way overestimates ability for average and below average people.  If the multiplier did not change, and there was just one constant linear progression, the game would do a good job of simulating very strong people as well. 

What is interesting to note is that the maximum amount that an unmodified human can lift in the game (960 lbs) is pretty close the maximum that any real human has lifted.  It is just that the game mechanic overestimates the proportion of people who can lift that much.  Perhaps far more people hit the gym really hard in the grim future of Rifts.  It is important to fill up that suit of armor covered in skulls and spikes.

Here is the table of carrying and lifting ability by Physical Strength score, and the proportions of characters who would have each score by rolling.

Dungeons and Dragons 3.5: Strength and Lifting

D&D 3.5, the d20 OGL line that spawned a flood of content, actually seems to have the most accurate simulation of human lifting ability.  I have almost finished making graphs for the systems I have, and 3.5 looks best so far.  I dislike Dungeons and Dragons in general, and this came as a surprise to me, but there you have it.  It still pretty consistently overestimates people's lifting abilities, even men's by about 5-70 lbs at each score, but it has an appropriate curve.

To better simulate a real person, figure out your character's strength using the table below, then add 2 to it.  For example, if you are simulating someone who can deadlift 300 pounds in real life, the table would assign the character a Strength score of 13, but a score of 15 is more appropriate based on the proportion of the population with that lifting ability.  Here is the table of encumbrance thresholds for 3.5.  Is this the same for Pathfinder?  I do not have the Pathfinder system, but I am under the impression that it uses the same rules as 3.5.

Dungeons and Dragons 4th edition: Strength and Lifting

Now that I've finished creating a reasonable distribution of real human lifting ability, I can compare it to the distributions generated by the mechanics of role-playing games.  Let us start with the 4th edition of Dungeons and Dragons.  Here is a table showing how lifting ability is calculated in-game based on the Strength attribute:

A character holding up to a "Normal" weight does not suffer encumbrance penalties. The rules say that characters can not lift more than the "Heavy" amount, though they can still move around while holding such weight. 

If we go back to the roots of D&D, when Strength was determined by rolling 3d6, we could  create proxy values of the proportions of the population with each Strength value (mean = 10.5).  Then we can graph the amount of weight that real persons could lift along with what D&D characters can lift:

The D&D rules provide a linear progression of lifting ability.  D&D 4th edition closely simulates real people's abilities at Strengths of 3 and 14-16, but gives a greater lifting ability than realistic for characters with Strengths of 4-13, and lesser for the highest human Strengths.  I threw the values for real men into the graph to see if D&D was a better simulator of just men, and it does (the sum of the differences between D&D values and real values is smaller).

Of course, D&D 4th edition uses a point-buy system for attributes, so there are no clear proportions of characters with each lifting ability.  Let us see what the percentiles would be of D&D characters at each Strength score if the game were an accurate simulation of real people (the 3d6 line is included just for reference):

 We can see that the average D&D character should have a Strength of 6 or 7 (not 10 or 11) for the game to simulate real people.  Only a quarter of characters would have Strength scores of 11 or higher.

Next up: another game's strength system gets compared to real life.

Adult Deadlifting Distribution

Here is the aggregation of men's and women's lifting abilities.  Again, the graph is inaccurate for the bottom percent or so, and the estimate equation only really applies to the 5th-95th percentiles.  I assumed a 52% proportion of women, not that it significantly affects the graph.

We can see a few distinct segments of data.  The bottom third is pretty exclusively made up of women who do not lift weights.  The middle third consists of untrained men, and women who weight train.  We see a sharp upward slope around the 73rd percentile, which is due to elite women weightlifters. The 78th to 98th percentiles, roughly, are made up of men who weight train, and the spike at the end is elite weightlifting men.

Even small children and the very weakest adults can still lift at least 20 lbs.  60 lbs is a good estimate for the 5th percentile.  The average adult (in the US) can lift up to 125 lbs.  People in the 81st percentile can lift double the average amount.  People in the 95th percentile can lift about 310 lbs.  Over 400 lbs is the territory of elite men and a handful of women.  Over 700 lbs is the territory of just a handful of men.

Again, there are unrealistic steps in the graph due to how the data was originally collected, and the smoother curve is probably more representative of the population. There should be a steep slope up from a low weight in the lowest few percentiles, but data is not available. 

Here is the same graph in kilograms:

Men's Maximum Deadlifting Distribution in Pounds with Equation

I figured it would be helpful to readers to revisit the distribution for men's deadlifts using pounds instead of kilograms.  Also, as I have been working on graphs for future posts, I have been tweaking equations that generate good estimates of what a person can lift at any percentile.

 It is important to note that the line was not calculated to be a best-fit to the data, and that was intentional.  I do not like how the deadlifting data I have creates a large jump past the 50th percentile, and it is entirely an artifact of the way the data was collected, not representative of the population, which would follow a smoother curve.  The equation I settled on is 65 + 35 * 1.0225 ^ (100 * percentile) in pounds.  Some day I will learn how to make equations pretty.  What is it, LaTeX?

Also, the equation for the line should only be used to estimate deadlifting ability for the 5th-95th percentiles.  Over the 95th, we see a sharp turn upward as the elites truly separate themselves from the pack.  Below the 5th percentile, we would also see a sharp turn downward if any data had been available for unhealthy or particularly weak men.  The lowest value available is the average maximum weight lifted by men with body weights in the bottom 0.005 proportion.

Women's Maximum Deadlifting Distribution

As I have done for men, I came up with a reasonable distribution of the lifting capabilities of US women.  Global data just is not available. The proportion of women who lift weights has nearly tripled over the last two decades to 21%, but this does not tell us what proportion weight-train with the goal of really getting strong.  I estimated some proportions to combine with the deadlifting table for women. 

It is interesting to note that any person can almost double what they can lift with six months of diligent training.  Also, the proportions of people rigorously training are fluid over time as weight-lifting fluctuates in popularity.  As women's sports have become more popular, and the health benefits of weight training become more obvious with increased scientific research, the curve in these graphs has become less acute, and may continue to straighten out a little in the future.  These graphs are snapshots in time, and do only apply to healthy women who have had the advantages of a first-world nation.  I've got these for you in pounds and kilograms, for your convenience. 

The strongest woman in the world has deadlifted 686 pounds (311 kg), so that is the current 0.000000001 level for women, and requires a life dedicated to building strength. 

For some clean RPG mechanic guidelines, the average woman can lift about 80 lbs (or let's say 35 kg).  A woman who is small and particularly weak should still be able to lift at least half as much.  Women at the 95th percentile can lift twice as much as an average woman.  The hard-training elite can lift four times the average.  These ratios are very similar to those for the men, except that the strongest woman in the world lifts almost nine times the average.

Next post: all adults together, which should really be the standard for developing RPG strength scales.

Women's and All Adult Weight Distributions

Continuing to use the EPA data, I plotted out a weight distribution for women.  Unlike the men's distribution, though, women's does not have a normally distributed natural log, so I filled in missing values without an equation.  The women's distribution has a more pronounced curve than men's.  I then figured overall adult weights by weighting and consolodating the men's and women's distributions with the assumption that our adult population is 52% women.

This information will be useful for players of games that take weight into consideration, such as Heavy Gear and Shadowrun.  Readers may want to keep in mind that people's weights peak in late middle age, and are lowest in early adulthood, with an average difference of about 15 lbs.  Also, there are racial differences.  Some supplementary information on racial differences (the EPA only lists Blacks and Whites) can be found here.

 

 The next step will be to find the proportion of women who weight-train, combine their weights with the deadlifting table, and plot women's deadlifting ability distribution, as well as for all adults, as I have already done for men.

Men's Maximum Deadlifting Distribution

Okay, still using the best source of strength data I could find, the distribution of men's body weights, and a scant article on a CDC study on the proportion of people who work out, I made a reasonable graph of the distribution of adult male maximum lifting ability.

Now, we know for a fact that there are dudes on this Earth who can lift over 400kg, but this graph only tracks up to the top 0.0001 of men.  About 0.00000001 of men can lift 450kg.  Also, I have no lifting data for the bottom 0.0034 of men, which should not be a big deal for RPG mechanics development.

Clearly, the average man can deadlift a max of ~80kg, or about 176 lbs.  The weakest men can still lift about half that, and men at the 95th percentile can lift about double that.  Elite lifters can handle three times as much as an average man, and the strongest men in the world can lift five times as much.  Those are some clean, easy guidelines for simulations. 

This graph is the predecessor of the top graph, and shows the same data with a different x scale:

I will eventually do this for women. Men tend to lift .42 to .64 more than women of the same body weight and same training.  Since men also tend to be heavier and lift weights more often, the women's distribution is probably about half of men's.

I will also compare the strength progressions of popular RPG systems to this real distribution, and rate them by how accurately they simulate real life, as well as by playability, of course.  I am using only deadlifts because nearly every system has rules for the maximum amount that a character can lift and not be able to move with, and most systems have no mechanics for other exercises.